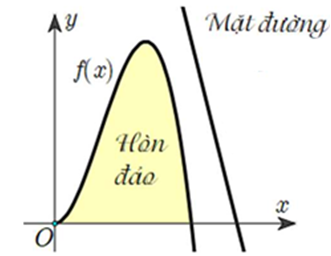
Cho hình phẳng 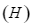 giới hạn bởi các đường
giới hạn bởi các đường 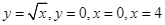 . Đường thẳng
. Đường thẳng 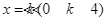 chia
chia 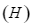 thành hai phần có diện tích
thành hai phần có diện tích 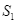 và
và 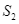 như hình vẽ.
như hình vẽ.
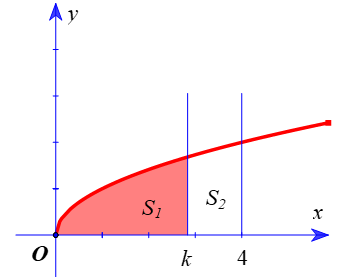
Biết 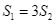 , tính giá trị của biểu thức
, tính giá trị của biểu thức 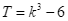 (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
Đáp án: _______
Cho hình phẳng ![]() giới hạn bởi các đường
giới hạn bởi các đường ![]() . Đường thẳng
. Đường thẳng ![]() chia
chia ![]() thành hai phần có diện tích
thành hai phần có diện tích ![]() và
và ![]() như hình vẽ.
như hình vẽ.

Biết ![]() , tính giá trị của biểu thức
, tính giá trị của biểu thức ![]() (nhập đáp án vào ô trống).
(nhập đáp án vào ô trống).
Đáp án: _______
Quảng cáo
Trả lời:
Đáp án đúng là "30"
Phương pháp giải
Diện hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng ![]() là
là 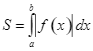 .
.
Lời giải
Diện tích hình ![]() là
là 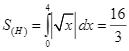 .
.
Diện tích ![]() là
là 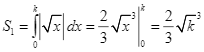
Để ![]() thì
thì ![]() .
.
Do đó ![]() .
.
Vậy ![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là A
Phương pháp giải
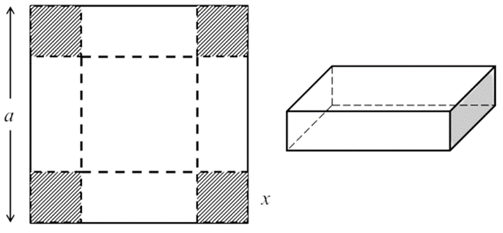
Lập hàm số thể tích cái hộp không nắp theo biến ![]() , sau đó tìm giá trị lớn nhất của hàm số vừa lập.
, sau đó tìm giá trị lớn nhất của hàm số vừa lập.
Lời giải
Cạnh đáy của cái hộp không nắp là ![]() . Điều kiện:
. Điều kiện: ![]() .
.
Thể tích của cái hộp không nắp là ![]()
Xét hàm số ![]() trên
trên ![]()
![]() liên tục trên
liên tục trên ![]()
![]()
![]() (loại)
(loại)
BBT
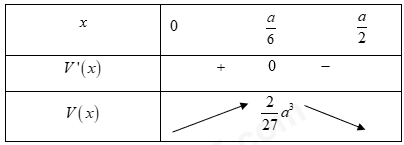
Dựa vào 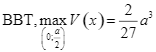 đạt tại
đạt tại ![]() . Khi đó, cạnh đáy của cái hộp là
. Khi đó, cạnh đáy của cái hộp là ![]() .
.
Lời giải
Đáp án đúng là B
Phương pháp giải
Công thức Bayes: 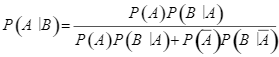 .
.
Lời giải
Gọi ![]() là biến cố "người được chọn nghiện thuốc lá".
là biến cố "người được chọn nghiện thuốc lá".
Gọi ![]() là biến cố "người được chọn bị bệnh phổi".
là biến cố "người được chọn bị bệnh phổi".
Ta cần tính ![]() .
.
Ta có: ![]() .
.
Theo công thức Bayes, ta có
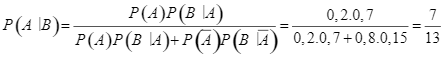
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. tháng 2 năm 2023.
C. tháng 4 năm 2023.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. tồn tại dưới dạng cation và di chuyển về cực âm (−) nguồn điện.
B. tồn tại dưới dạng anion và di chuyển về cực dương (+) nguồn điện.
C. tồn tại dưới dạng anion và di chuyển về cực âm (−) nguồn điện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 0,31(s)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.