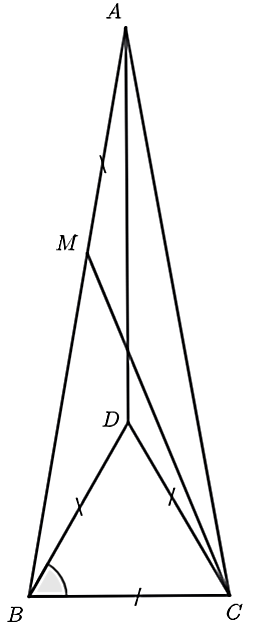
Cho \(\Delta ABC\) có \(\widehat A = 20^\circ \) có \(AB = AC\), lấy \(M \in AB\) sao cho \(MA = BC\). Số đo \(\widehat {AMC}\) bằng bao nhiêu độ?
Cho \(\Delta ABC\) có \(\widehat A = 20^\circ \) có \(AB = AC\), lấy \(M \in AB\) sao cho \(MA = BC\). Số đo \(\widehat {AMC}\) bằng bao nhiêu độ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Hướng dẫn giải Đáp án: \(150\) Dựng \(\Delta BDC\) đều (\(D,A\) cùng phía so với \(BC\)). Nối \(A\) với \(D\). Xét \(\Delta ABD\) và \(\Delta CDA\), có: \(AB = AC\) (gt) \(DA\) chung (gt) \(AD = DC\) (gt) Ta có \(\Delta ABD = \Delta CDA\) (c.c.c) nên \(\widehat {DAC} = \widehat {DAB} = 10^\circ \). Xét \(\Delta AMC\) và \(\Delta CDA\), có: \(AM = DC\) (gt) \(\widehat A\) chung (gt) \(AM\) chung (gt) Do đó, \(\Delta AMC = \Delta CDA\) (c.g.c) nên \(\widehat {MCA} = \widehat {DAC} = 10^\circ \) (hai góc tương ứng) Suy ra \(\widehat {AMC} = 180^\circ - \left( {\widehat {ACM} + \widehat {MAC}} \right) = 180^\circ - \left( {20^\circ + 10^\circ } \right) = 150^\circ \). |
|
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Ta có hai số tự nhiên liên tiếp cách nhau \(2\) đơn vị.
Do đó, biểu thức biểu thị tổng của hai số tự nhiên lẻ liên tiếp \(x + \left( {x + 2} \right)\) với \(x = 2k + 1,k \in \mathbb{N}.\)
Lời giải
Ta có đa thức \(A\left( x \right)\) có bậc là 3.
Có: \(H\left( x \right) = A\left( x \right) + B\left( x \right) = 2{x^3} - 5{x^2} - 7x - 2023 + \left( { - 2} \right){x^3} + 9{x^2} + 7x + 2024\)
\( = \left( {2{x^3} - 2{x^3}} \right) + \left( { - 5{x^2} + 9{x^2}} \right) + \left( {7x - 7x} \right) - 2023 + 2024\)
\( = {x^2} + 1\).
Vậy \(H\left( x \right) = {x^2} + 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo