Câu hỏi:
21/04/2025 157
Câu 1-3. (1,5 điểm) Cho biểu thức .
a) Tìm điều kiện xác định của biểu thức \(M\).
Câu 1-3. (1,5 điểm) Cho biểu thức .
a) Tìm điều kiện xác định của biểu thức \(M\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Điều kiện: \[\left\{ \begin{array}{l}{x^2} - 7x + 10 \ne 0\\{x^2} - 4 \ne 0\\2 - x \ne 0\end{array} \right.\] nên \[\left\{ \begin{array}{l}\left( {x - 2} \right)\left( {x - 5} \right) \ne 0\\\left( {x + 2} \right)\left( {x - 2} \right) \ne 0\\x \ne 2\end{array} \right.\], do đó \[\left\{ \begin{array}{l}x \ne - 2\\x \ne 2\\x \ne 5\end{array} \right.\].
Vậy điều kiện xác định của biểu thức \(M\) là \[x \ne - \,2;\,\,x \ne \,2;\,\,x \ne 5\].
Câu hỏi cùng đoạn
Câu 2:
b) Rút gọn biểu thức \(M\).
b) Rút gọn biểu thức \(M\).
Lời giải của GV VietJack
b) Với \[x \ne - \,2;\,\,x \ne \,2;\,\,x \ne 5\], ta có:
\[M = \frac{{2x - 10}}{{{x^2} - 7x + 10}} - \frac{{2x}}{{{x^2} - 4}} + \frac{1}{{2 - x}} = \frac{{2\left( {x - 5} \right)}}{{\left( {x - 2} \right)\left( {x - 5} \right)}} - \frac{{2x}}{{{x^2} - 4}} - \frac{1}{{x - 2}}\]
\[ = \frac{2}{{x - 2}} - \frac{1}{{x - 2}} - \frac{{2x}}{{{x^2} - 4}} = \frac{1}{{x - 2}} - \frac{{2x}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\]
\[ = \frac{1}{{x - 2}} - \frac{{2x}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} = \frac{{x + 2}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} - \frac{{2x}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}\]
\[ = \frac{{2 - x}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} = \frac{{ - 1}}{{x + 2}}\].
Vậy \(M = \frac{{ - 1}}{{x + 2}}\).
Câu 3:
c) Tìm giá trị nguyên của \(x\) để \(M\) nhận giá trị nguyên.
c) Tìm giá trị nguyên của \(x\) để \(M\) nhận giá trị nguyên.
Lời giải của GV VietJack
c) Để \(M\) nhận giá trị nguyên thì \(x + 2 \in \)Ư\(\left( { - 1} \right)\).
Suy ra \(x + 2 \in \left\{ { - 1\,;\,\,1} \right\}\) hay \(x \in \left\{ { - 3\,;\,\, - 1} \right\}\) (TMĐK).
Vậy với \(x \in \left\{ { - 3\,;\,\, - 1} \right\}\) thì \(M\) nhận giá trị nguyên.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
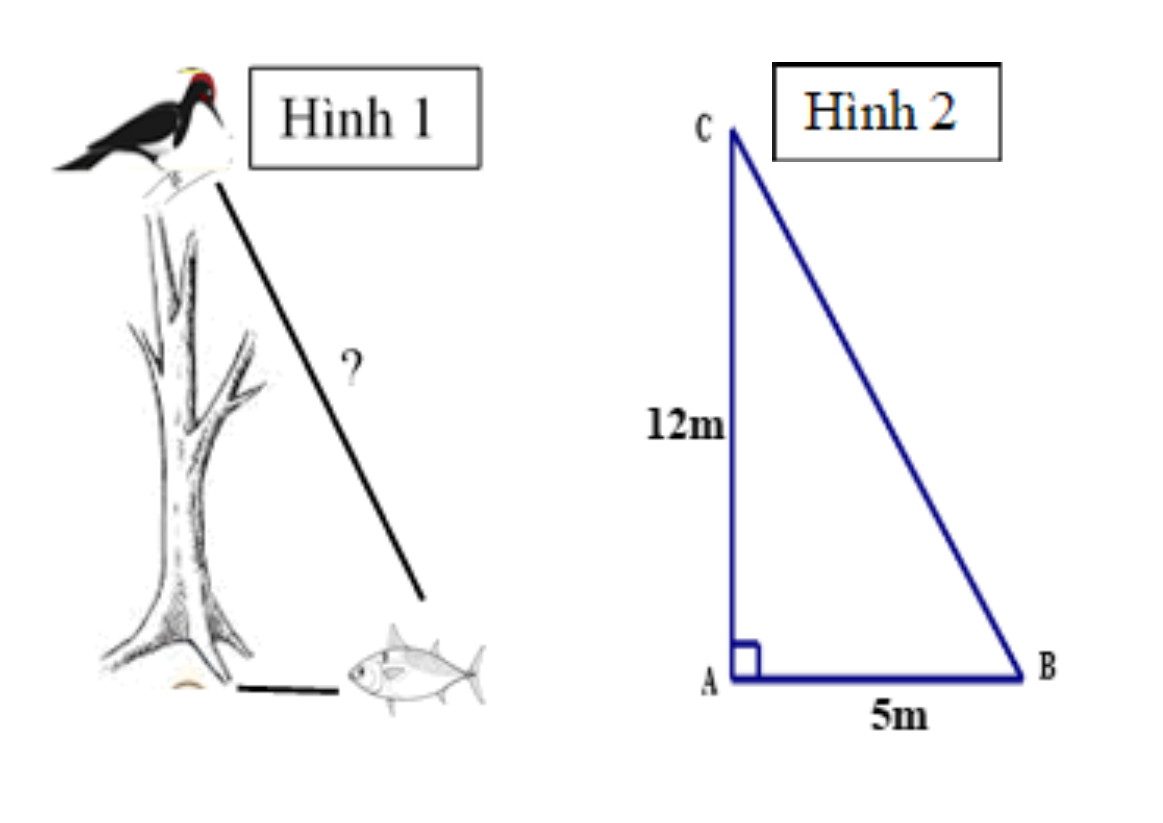
Xét \(\Delta ABC\) vuông tại \[A\], theo định lý Pythagore, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {12^2} = 25 + 144 = 169.\)
Suy ra \[BC = 13\,\,{\rm{m}}{\rm{.}}\]
Vậy con chim bay được một đoạn bằng \[13\,\,{\rm{m}}\] thì bắt được con cá.
Lời giải
a) Xét \[\Delta ABH\] và \[\Delta CBA\] có:
\(\widehat {ABH} = \widehat {CBA}\); \(\widehat {AHB} = \widehat {CAB}\;\left( { = 90^\circ } \right)\)
Do đó .
Suy ra \(\frac{{AB}}{{CB}} = \frac{{BH}}{{BA}}\) hay \(A{B^2} = BH \cdot BC\) (đpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận