Câu hỏi:
21/04/2025 687
Câu 12-13. (1,5 điểm)
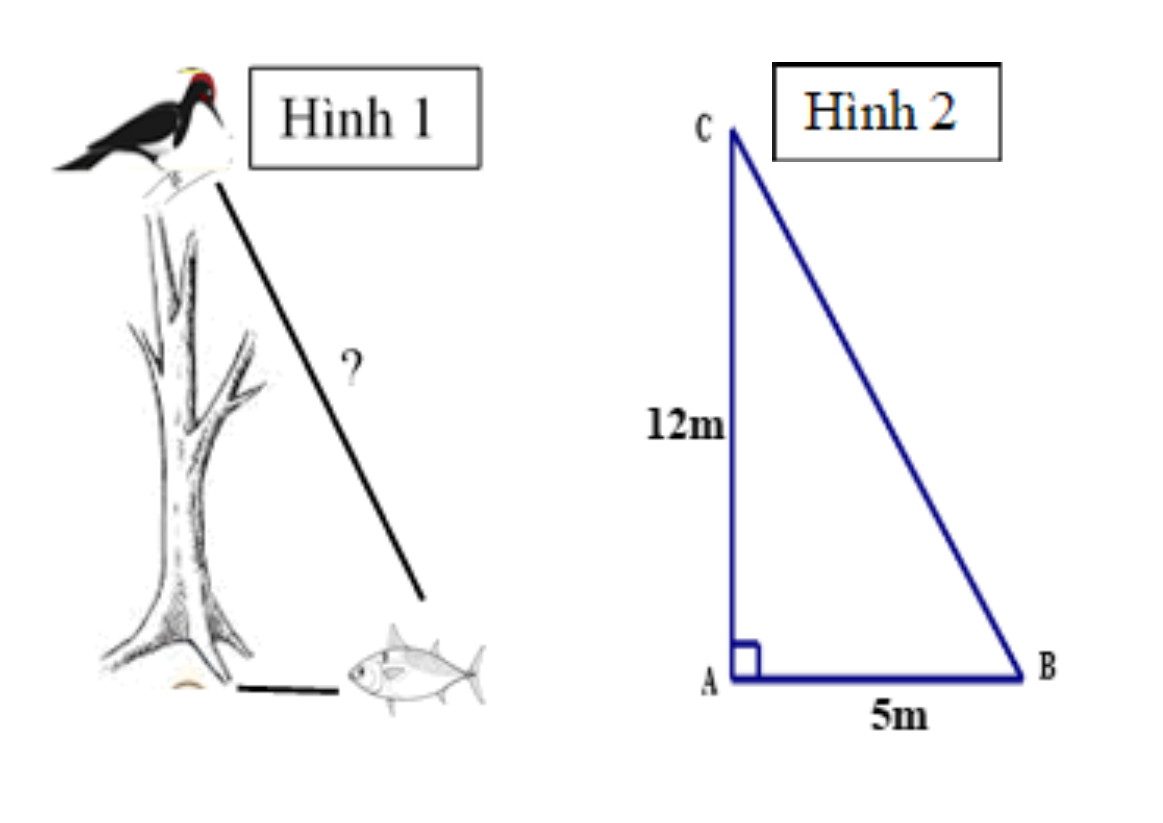
Một cây cao \[12\,\,{\rm{m}}\] mọc cạnh bờ sông. Trên đỉnh cây có một con chim đang đậu và chuẩn bị sà xuống bắt con cá trên mặt nước (như Hình 1 và được mô phỏng như Hình 2). Hỏi con chim sẽ bay một đoạn ngắn nhất bằng bao nhiêu mét thì bắt được con cá? (Biết con cá cách gốc cây \[5\,\,{\rm{m}}\] và nước cao mấp mé bờ sông).
Câu 12-13. (1,5 điểm)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét \(\Delta ABC\) vuông tại \[A\], theo định lý Pythagore, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {12^2} = 25 + 144 = 169.\)
Suy ra \[BC = 13\,\,{\rm{m}}{\rm{.}}\]
Vậy con chim bay được một đoạn bằng \[13\,\,{\rm{m}}\] thì bắt được con cá.
Câu hỏi cùng đoạn
Câu 2:
Một chiếc lều có hình dạng là một hình chóp tứ giác đều. Biết chiếc lều có mặt bên là tam giác đều có cạnh bằng \(2\,\,{\rm{m}}\). Tính chiều cao của chiếc lều.
Một chiếc lều có hình dạng là một hình chóp tứ giác đều. Biết chiếc lều có mặt bên là tam giác đều có cạnh bằng \(2\,\,{\rm{m}}\). Tính chiều cao của chiếc lều.
Lời giải của GV VietJack
Xét \(\Delta SAE\) vuông tại \(E\) có: \(S{E^2} + E{A^2} = S{A^2}\)
Suy ra \(S{E^2} = S{A^2} - E{A^2}\) \( = {2^2} - {1^2} = 3\).
Ta có \(SE\) là trung đoạn nên \(E\) là trung điểm của \(AB\).
Xét \(\Delta ABD\) có \(E,\,\,H\) lần lượt là trung điểm của \(AB,\,\,BD\).
Do đó \(EH\) là đường trung bình của \(\Delta ABD\) nên \(EH = \frac{1}{2}AD = 1\,\,\left( {\rm{m}} \right)\).
Xét \(\Delta SEH\) vuông tại \(H\) có: \(S{E^2} = S{H^2} + E{H^2}\) .
Suy ra \(S{H^2} = S{E^2} - E{H^2}\) \( = 3 - {1^2} = 2\).
Do đó \(SH = \sqrt 2 \,\,{\rm{m}}\).
Vậy chiều cao của chiếc lều là \(\sqrt 2 \,\,{\rm{m}}\,{\rm{.}}\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
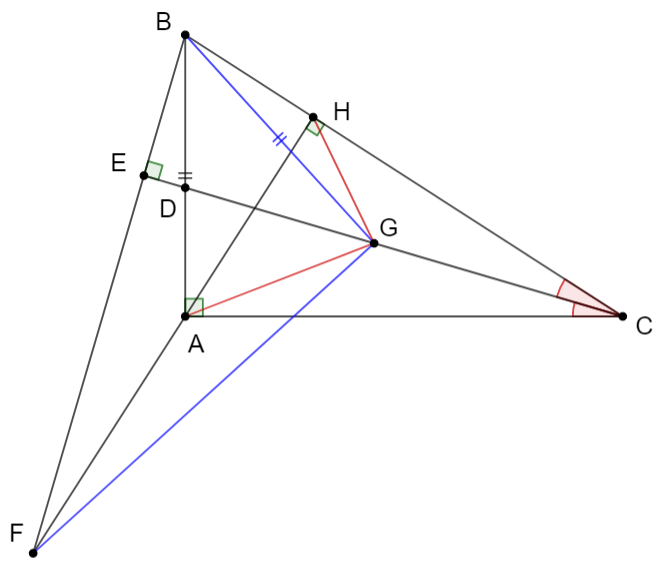
a) Xét \[\Delta ABH\] và \[\Delta CBA\] có:
\(\widehat {ABH} = \widehat {CBA}\); \(\widehat {AHB} = \widehat {CAB}\;\left( { = 90^\circ } \right)\)
Do đó .
Suy ra \(\frac{{AB}}{{CB}} = \frac{{BH}}{{BA}}\) hay \(A{B^2} = BH \cdot BC\) (đpcm)
Lời giải
Tổng khối lượng các loại hạt điều thu hoạch được là:
\(1\,\,450 + 2\,\,230 + 1\,\,860 = 5\,\,540\) (kg).
Vậy tổng khối lượng các loại hạt điều thu hoạch được là \(5\,\,540\) kg.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận