Câu hỏi:
21/04/2025 277
Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] vuông tại \[A\], đường cao \[AH\,\,\left( {H \in BC} \right)\]. Biết \[AB = 18{\rm{ cm,}}\] \[AC = 24{\rm{ cm}}{\rm{.}}\]
a) Chứng minh: \[A{B^2} = BH \cdot BC\].
Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] vuông tại \[A\], đường cao \[AH\,\,\left( {H \in BC} \right)\]. Biết \[AB = 18{\rm{ cm,}}\] \[AC = 24{\rm{ cm}}{\rm{.}}\]
a) Chứng minh: \[A{B^2} = BH \cdot BC\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
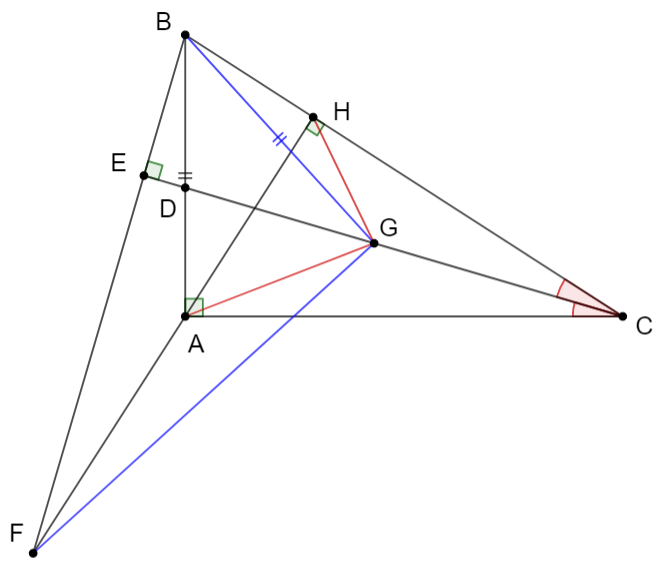
a) Xét \[\Delta ABH\] và \[\Delta CBA\] có:
\(\widehat {ABH} = \widehat {CBA}\); \(\widehat {AHB} = \widehat {CAB}\;\left( { = 90^\circ } \right)\)
Do đó .
Suy ra \(\frac{{AB}}{{CB}} = \frac{{BH}}{{BA}}\) hay \(A{B^2} = BH \cdot BC\) (đpcm)
Câu hỏi cùng đoạn
Câu 2:
b) Kẻ đường phân giác \[CD\] của tam giác \[ABC\]\[\left( {D \in AB} \right)\]. Tính độ dài \[DA\].
b) Kẻ đường phân giác \[CD\] của tam giác \[ABC\]\[\left( {D \in AB} \right)\]. Tính độ dài \[DA\].
Lời giải của GV VietJack
b) Áp dụng định lý Pythagore vào tam giác \[ABC\] vuông tại \[A\] có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{18}^2} + {{24}^2}} = 30\,\;{\rm{(cm)}}\).
Áp dụng tính chất đường phân giác với \[CD\] là đường phân giác của \[\widehat {ACB}\] nên
\(\frac{{DA}}{{BD}} = \frac{{AC}}{{BC}} = \frac{{24}}{{30}} = \frac{4}{5}\) hay \(BD = \frac{5}{4}DA\).
Lại có \[BD + DA = BA = 18\]
\(\frac{5}{4}DA + DA = 18\)
\(\frac{9}{4}DA = 18\)
\(DA = 18 \cdot \frac{4}{9} = 8\;\,{\rm{(cm)}}\).
Câu 3:
c) Từ \[B\] kẻ đường thẳng vuông góc với đường thẳng \[CD\] tại \[E\] và cắt đường thẳng \[AH\] tại \[F.\] Trên đoạn thẳng \[CD\] lấy điểm \[G\] sao cho \[BA = BG\]. Chứng minh: \[BG \bot FG\].
c) Từ \[B\] kẻ đường thẳng vuông góc với đường thẳng \[CD\] tại \[E\] và cắt đường thẳng \[AH\] tại \[F.\] Trên đoạn thẳng \[CD\] lấy điểm \[G\] sao cho \[BA = BG\]. Chứng minh: \[BG \bot FG\].
Lời giải của GV VietJack
c) Ta có \(\frac{{AB}}{{CB}} = \frac{{BH}}{{BA}}\;\left( {{\rm{cmt}}} \right)\) nên \(\frac{{BG}}{{CB}} = \frac{{BH}}{{BG}}\) suy ra \[B{G^2} = BH \cdot BC{\rm{ }}\,\,\left( 1 \right)\]
• Xét \[\Delta EBC\] và \[\Delta HBF\] có:
\[\widehat {BEC} = \widehat {BHF}\;\left( { = 90^\circ } \right)\]; \[\widehat {EBC} = \widehat {HBF}\].
Do đó
Suy ra \(\frac{{BH}}{{BE}} = \frac{{BF}}{{BC}}\) hay \(BH \cdot BC = BE \cdot BF\) (2)
Từ (1) và (2) suy ra \[B{G^2} = BE \cdot BF\] hay \(\frac{{BG}}{{BE}} = \frac{{BF}}{{BG}}.\)
• Xét \[\Delta BGE\] và \[\Delta BFG\] có
\[\frac{{BG}}{{BE}} = \frac{{BF}}{{BG}}\;\,\left( {{\rm{cmt}}} \right)\]; \[\widehat {EBG} = \widehat {GBF}\].
Do đó
Suy ra \(\widehat {BEG} = \widehat {BGF}\) (hai góc tương ứng)
Mà \(\widehat {BEG} = \widehat {BEC} = 90^\circ \) nên \(\widehat {BGF} = 90^\circ \).
Do đó \[BG \bot FG\] (đpcm).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
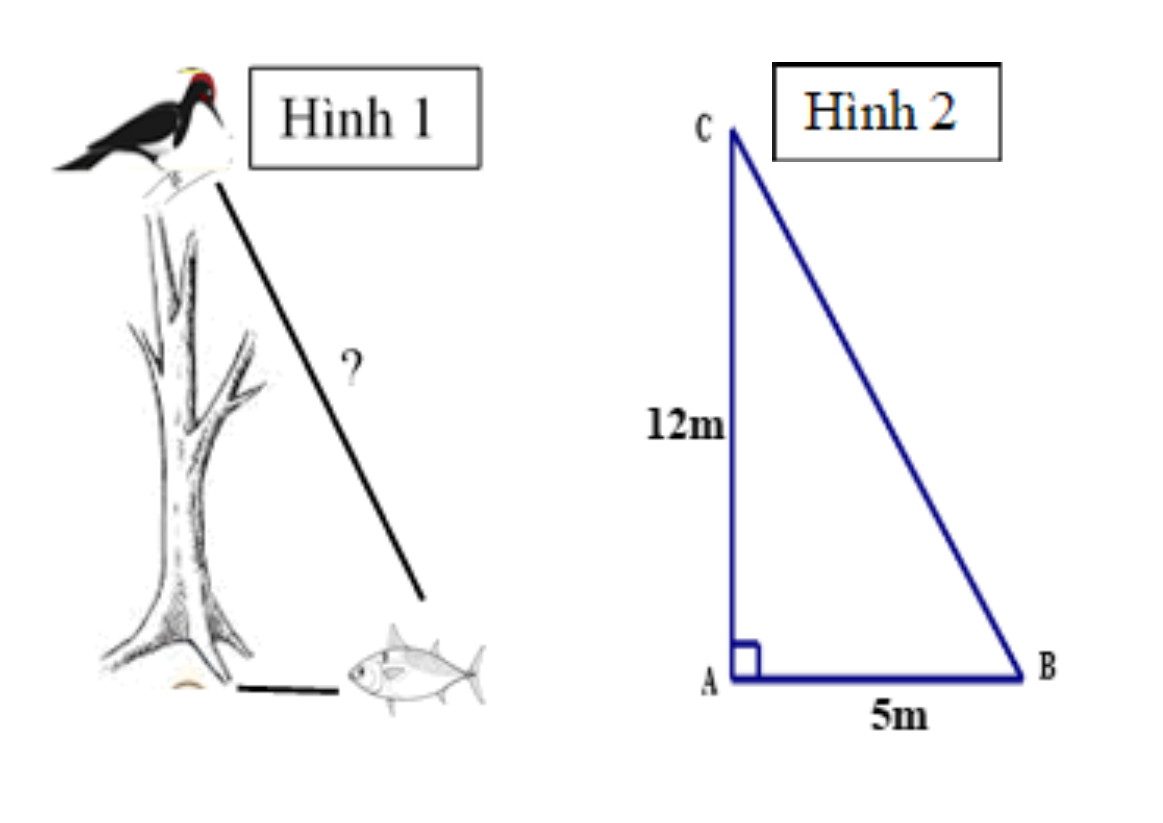
Xét \(\Delta ABC\) vuông tại \[A\], theo định lý Pythagore, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {12^2} = 25 + 144 = 169.\)
Suy ra \[BC = 13\,\,{\rm{m}}{\rm{.}}\]
Vậy con chim bay được một đoạn bằng \[13\,\,{\rm{m}}\] thì bắt được con cá.
Lời giải
Tổng khối lượng các loại hạt điều thu hoạch được là:
\(1\,\,450 + 2\,\,230 + 1\,\,860 = 5\,\,540\) (kg).
Vậy tổng khối lượng các loại hạt điều thu hoạch được là \(5\,\,540\) kg.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận