Câu hỏi:
21/04/2025 164
Câu 6 - 8. (1,5 điểm) Bạn An gieo xúc xắc 80 lần. Bạn An đếm được có 13 lần xuất hiện mặt 2 chấm, 12 lần xuất hiện mặt 4 chấm và 14 lần xuất hiện mặt 6 chấm.
a) Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số 4”.
Câu 6 - 8. (1,5 điểm) Bạn An gieo xúc xắc 80 lần. Bạn An đếm được có 13 lần xuất hiện mặt 2 chấm, 12 lần xuất hiện mặt 4 chấm và 14 lần xuất hiện mặt 6 chấm.
a) Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số 4”.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số 4” là \(\frac{{12}}{{80}} = \frac{3}{{20}}.\)
Câu hỏi cùng đoạn
Câu 2:
b) Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ”.
b) Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ”.
Lời giải của GV VietJack
b) Số lần xúc xắc xuất hiện số lẻ là: \(80 - 13 - 12 - 14 = 41\) (lần).
Xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ” là \(\frac{{41}}{{80}}.\)
Câu 3:
c) Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ” với xác suất của biến cố đó khi số lần gieo ngày càng lớn.
c) Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ” với xác suất của biến cố đó khi số lần gieo ngày càng lớn.
Lời giải của GV VietJack
c) Trong các số chấm từ 1 chấm đến 6 chấm, thì có 3 mặt có số chấm là số lẻ.
Do đó xác suất của biến cố “Mặt xuất hiện của xúc xắc là số lẻ” là \(\frac{3}{6} = \frac{1}{2}.\)
Vậy khi số lần gieo ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ” càng gần với \(\frac{1}{2}.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
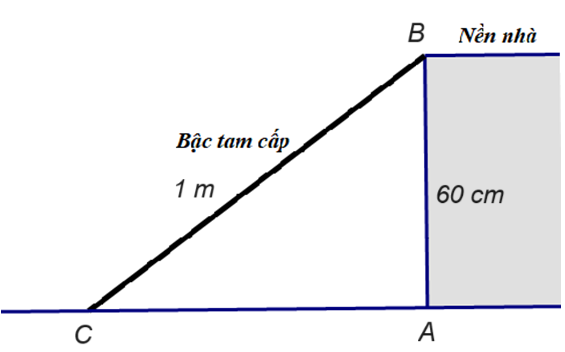
Xét \(\Delta ABC\) vuông tại \[A\], theo định lý Pythagore, ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
Suy ra \[A{C^2} = B{C^2} - A{B^{2\;}} = {100^2} - {60^2} = 6400\].
Khi đó \[AC = \sqrt {6\,400} = 80\,\,{\rm{(cm)}}\]
Vì \[80\,\,{\rm{cm}} < 85\,\,{\rm{cm}}\] nên nhà bạn Nam đã thực hiện đúng quy định của khu phố.
Lời giải
a) Xét \[\Delta ABK\] và \[\Delta CBF\] có:
\[\widehat {ABK} = \widehat {CBF}\;\left( {\widehat B\;\,{\rm{chung}}} \right)\]; \(\widehat {AKB} = \widehat {CFB}\;\left( { = 90^\circ } \right)\)
Do đó
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận