Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\]
a) Chứng minh: .
Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\]
a) Chứng minh: .
Quảng cáo
Trả lời:
Giải bởi Vietjack
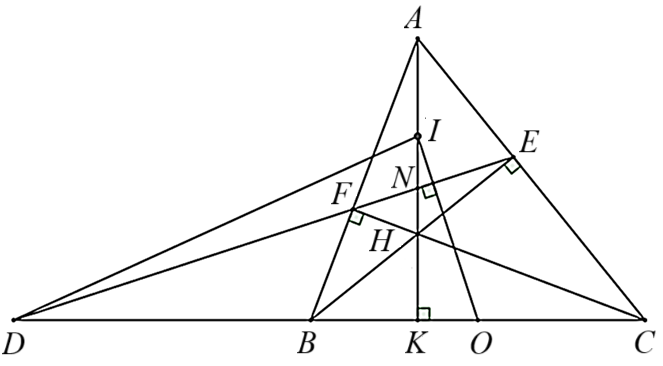
a) Xét \[\Delta ABK\] và \[\Delta CBF\] có:
\[\widehat {ABK} = \widehat {CBF}\;\left( {\widehat B\;\,{\rm{chung}}} \right)\]; \(\widehat {AKB} = \widehat {CFB}\;\left( { = 90^\circ } \right)\)
Do đóCâu hỏi cùng đoạn
Câu 2:
b) Chứng minh: \(AE \cdot AC = AF \cdot AB\).
b) Chứng minh: \(AE \cdot AC = AF \cdot AB\).
Giải bởi Vietjack
b) Xét \[\Delta AEB\] và \[\Delta ACF\] có:
\(\widehat {EAB} = \widehat {FAC}\;\,\left( {\widehat A\;\,{\rm{chung}}} \right)\); \(\widehat {AEB} = \widehat {AFC}\;\left( { = 90^\circ } \right)\)
Do đóSuy ra \(\frac{{AE}}{{AF}} = \frac{{AB}}{{AC}}\) hay \(AE \cdot AC = AF \cdot AB\) (đpcm)
Câu 3:
c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\]
c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\]
Giải bởi Vietjack
c) Xét \[\Delta BFC\] vuông tại \[F\] có \[O\] là trung điểm của \[BC\] nên \(FO = \frac{{BC}}{2}\).
Xét \[\Delta BEC\] vuông tại \[E\] có \[O\] là trung điểm của \[BC\] nên \(EO = \frac{{BC}}{2}\).
Do đó \[FO = EO = \frac{{BC}}{2}\]. (1)
Xét \[\Delta AEH\] vuông tại \[E\] có \[I\] là trung điểm của \[AH\] nên \(EI = \frac{{AH}}{2}\).
Xét \[\Delta AFH\] vuông tại \[F\] có \[I\] là trung điểm của \[AH\] nên \(FI = \frac{{AH}}{2}\).
Do đó \[FI = EI = \frac{{AH}}{2}\]. (2)
Từ (1) và (2) ta suy ra được \[OI\] là đường trung trực của cạnh \[EF\].
Khi đó \[OI \bot EF\] hay \[OI \bot DN\].
Do đó \[DN\] là đường cao của \[\Delta DOI\].
Xét \[\Delta DOI\] có \[DN\] và \[IK\] là đường cao và \[N\] là giao của \[DN\] và \[IK\].
Do đó \[N\] là trực tâm của tam giác \[DOI\].
Vậy \[OI \bot DI\] (đpcm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
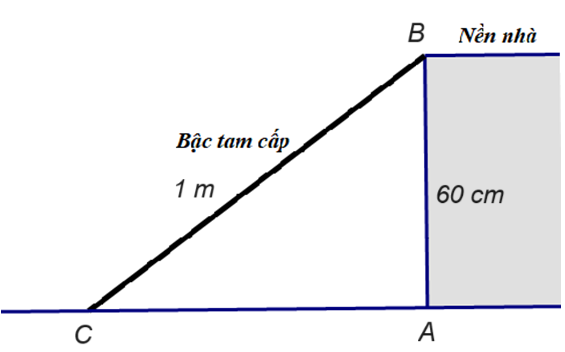
Xét \(\Delta ABC\) vuông tại \[A\], theo định lý Pythagore, ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
Suy ra \[A{C^2} = B{C^2} - A{B^{2\;}} = {100^2} - {60^2} = 6400\].
Khi đó \[AC = \sqrt {6\,400} = 80\,\,{\rm{(cm)}}\]
Vì \[80\,\,{\rm{cm}} < 85\,\,{\rm{cm}}\] nên nhà bạn Nam đã thực hiện đúng quy định của khu phố.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Ta có \({x^3} - 1 = \left( {x - 1} \right)\left( {{x^2} + x + 1} \right).\)
\[{x^2} + x + 1 = {\left( {x + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0.\]
Điều kiện: \[\left\{ \begin{array}{l}{x^3} - 1 \ne 0\\x - 1 \ne 0\end{array} \right.\] nên \[\left\{ \begin{array}{l}\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) \ne 0\\x - 1 \ne 0\end{array} \right.\], do đó \[x \ne 1\].
Vậy điều kiện xác định của biểu thức \(P\) là \[x \ne 1\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập