Câu hỏi:
24/04/2025 33
Dựa vào thông tin dưới đây để trả lời các câu từ 67 đến 69
Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} - 3x - 6\ln \left( {2 - x} \right) + 1\).
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
Dựa vào thông tin dưới đây để trả lời các câu từ 67 đến 69
Cho hàm số \(f\left( x \right) = \frac{{{x^3}}}{3} - 3x - 6\ln \left( {2 - x} \right) + 1\).
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tập xác định của hàm số là \(\left( { - \infty \,;\,2} \right)\).
Ta có \(f'\left( x \right) = {x^2} - 3 + \frac{6}{{2 - x}} = \frac{{{x^3} - 2{x^2} - 3x}}{{x - 2}} = \frac{{x\left( {x + 1} \right)\left( {x - 3} \right)}}{{x - 2}},\,\forall x \in \left( { - \infty ;2} \right)\).
Trên khoảng \(\left( { - \infty \,;\,2} \right)\), \(f'\left( x \right) = 0 \Leftrightarrow x = - 1\) hoặc \(x = 0\).
Bảng biến thiên của hàm số như sau:
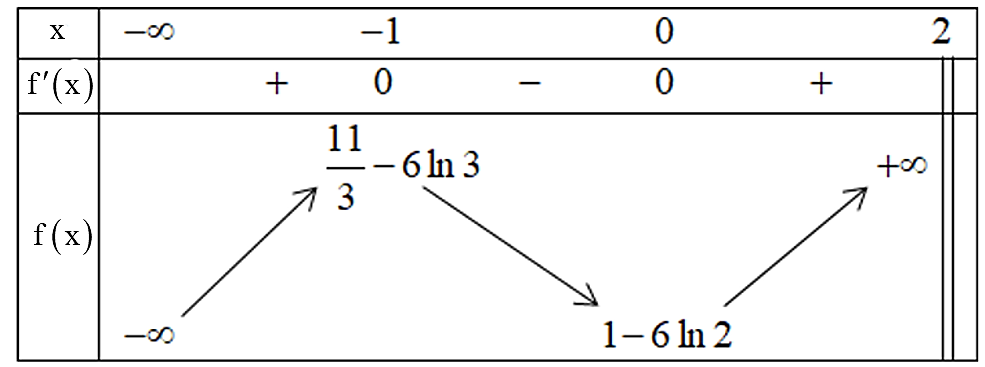
Dựa vào bảng biến thiên, ta có hàm số đồng biến trên các khoảng \(\left( { - \infty ;\, - 1} \right)\) và \(\left( {0\,;\,2} \right)\). Chọn B.
Câu hỏi cùng đoạn
Câu 2:
Tổng các giá trị cực đại và cực tiểu của hàm số bằng
Đáp án chính xác
Lời giải của GV VietJack
Từ bảng biến thiên của hàm số ta có hàm số đạt cực đại tại \(x = - 1\), ; hàm số đạt cực tiểu tại \(x = 0\), \({y_{CT}} = 1 - 6\ln 2\).
Vậy . Chọn A.
Câu 3:
Đồ thị hàm số \(g\left( x \right) = \frac{{f\left( x \right)}}{{{x^2} + 2x + 2}}\) có đường tiệm cận xiên có dạng \(y = ax + b\). Khi đó giá trị của biểu thức \(a + b\) là:
Đáp án chính xác
Lời giải của GV VietJack
Hàm số \(g\left( x \right) = \frac{{f\left( x \right)}}{{{x^2} + 2x + 2}}\).
Ta có \(\mathop {\lim }\limits_{x \to - \infty } \frac{{g\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\frac{{{x^3}}}{3} - 3x - 6\ln \left( {2 - x} \right) + 1}}{{x\left( {{x^2} + 2x + 2} \right)}} = \frac{1}{3} = a\).
Khi đó, \(\mathop {\lim }\limits_{x \to - \infty } \left( {g\left( x \right) - \frac{1}{3}x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{\frac{{{x^3}}}{3} - 3x - 6\ln \left( {2 - x} \right) + 1}}{{{x^2} + 2x + 2}} - \frac{1}{3}x} \right)\)
\( = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - 2{x^2} - 11x - 18\ln \left( {2 - x} \right) + 3}}{{3\left( {{x^2} + 2x + 2} \right)}}} \right) = - \frac{2}{3} = b\).
Vậy \(a + b = - \frac{1}{3}\). Chọn B.
Nhà sách vietjack
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Dựa vào thông tin dưới đây để trả lời các câu từ 76 đến 77
Trong một ngôi làng có 500 người thì 240 người là nam. Thống kê cho thấy rằng, khả năng mắc bệnh hô hấp ở người nam trong làng là 0,6% và ở người nữ trong làng là 0,35%. Giả sử gặp một người trong làng.
Tỉ lệ mắc bệnh hô hấp chung của cả làng là:
Dựa vào thông tin dưới đây để trả lời các câu từ 76 đến 77
Trong một ngôi làng có 500 người thì 240 người là nam. Thống kê cho thấy rằng, khả năng mắc bệnh hô hấp ở người nam trong làng là 0,6% và ở người nữ trong làng là 0,35%. Giả sử gặp một người trong làng.
Tỉ lệ mắc bệnh hô hấp chung của cả làng là:
Xem đáp án »
24/04/2025
98
🔥 Đề thi HOT:
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 1)
-
(2025) Đề thi thử Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG TP.HCM - Sử dụng ngôn ngữ Tiếng Việt - Chính tả
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 3)
-
(2025) Đề thi thử Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 2)
-
(2025) Đề minh họa Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án ( Đề 8)
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 4)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận