Linh có 39 viên bi được chia làm 3 nhóm như ảnh dưới đây.
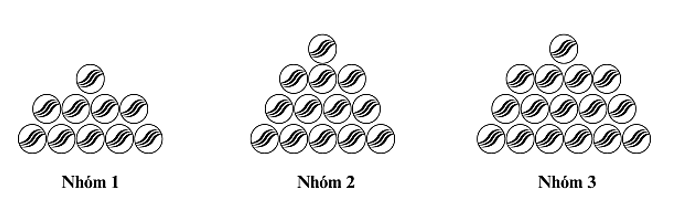
Bằng cách thay đổi vị trí của các viên bi, Linh đảm bảo rằng số lượng viên bi trong ba nhóm từ trái qua phải trở thành 3 số hạng liên tiếp của một cấp số nhân với công bội dương khác 1. Hỏi Linh phải di chuyển ít nhất bao nhiêu viên bi?
Linh có 39 viên bi được chia làm 3 nhóm như ảnh dưới đây.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giả sử số bi ở 3 nhóm lần lượt là \({u_1}\,;\,{u_1} \cdot q\,;\,{u_1} \cdot {q^2}\,\,\left( {{u_1} \in {\mathbb{N}^*},\,q > 0\,,\,q \ne 1} \right)\). Khi đó ta có:
\({u_1} + {u_1}q + {u_1}{q^2} = 39 \Rightarrow {u_1} = \frac{{39}}{{1 + q + {q^2}}}\).
Do \({u_1} \in {\mathbb{N}^*}\) nên \(1 + q + {q^2} = 3\) hoặc \(1 + q + {q^2} = 13\).
Trường hợp 1. Với \(1 + q + {q^2} = 3 \Leftrightarrow {q^2} + q - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}q = 1\\q = - 2\end{array} \right.\) (loại).
Trường hợp 2. Với \(1 + q + {q^2} = 13 \Leftrightarrow {q^2} + q - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}q = 3\\q = - 4\end{array} \right. \Rightarrow q = 3 \Rightarrow {u_1} = 3\). Khi đó số bi 3 nhóm lần lượt 3; 9; 27.
Do đó cần di chuyển 7 bi từ nhóm 1 sang nhóm 3 và 4 bi từ nhóm 2 sang nhóm 3.
Vậy số bị cần di chuyển tối thiểu là 11 bi. Chọn D.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Gọi biến cố C: “Đội tuyển chỉ thắng có một trận”.
Ta có \(P\left( C \right) = P\left( {A\bar B} \right) + P\left( {\bar AB} \right) = P\left( A \right) - P\left( {AB} \right) + P\left( B \right) - P\left( {AB} \right)\)
\( = P\left( A \right) + P\left( B \right) - 2P\left( {AB} \right) = 0,8 + 0,54 - 2 \cdot 0,6 \cdot 0,8 = 0,38\). Chọn C.
Câu 2
Lời giải
Xét các biến cố A: “Vận động viên A thắng trận”, B: “Vận động viên B thắng trận”.
Theo bài ra ta có: \(P\left( A \right) = 0,8;\,\,P\left( {B|A} \right) = 0,6;\,\,P\left( {B|\bar A} \right) = 0,3\). Suy ra \(P\left( {\bar A} \right) = 0,2\).
Xác suất B thắng trận là: \(P\left( B \right) = P\left( A \right) \cdot P\left( {B|A} \right) + P\left( {\bar A} \right) \cdot P\left( {B|\bar A} \right) = 0,54\). Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập