Câu hỏi:
25/04/2025 10
Dựa vào thông tin dưới đây để trả lời các câu từ 80 đến 81
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy ABC là tam giác vuông tại A, \(AB = a,\,BC = 2a\). Mặt bên \(ABB'A'\) là hình thoi, mặt bên \(BCC'B'\) nằm trong mặt phẳng vuông góc với đáy, hai mặt này hợp với nhau một góc a.
Thể tích khối lăng trụ \(ABC.A'B'C'\) là:
Dựa vào thông tin dưới đây để trả lời các câu từ 80 đến 81
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy ABC là tam giác vuông tại A, \(AB = a,\,BC = 2a\). Mặt bên \(ABB'A'\) là hình thoi, mặt bên \(BCC'B'\) nằm trong mặt phẳng vuông góc với đáy, hai mặt này hợp với nhau một góc a.
Thể tích khối lăng trụ \(ABC.A'B'C'\) là:
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
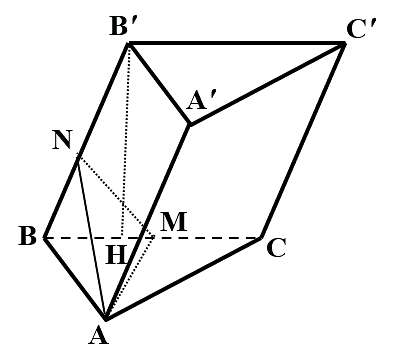
Kẻ MN vuông góc với \(BB'\) suy ra \(\widehat {ANM} = \alpha \).
Hạ \(B'H \bot BC\) thì \(B'H \bot \left( {ABC} \right)\) nên
\({V_{ABC.A'B'C'}} = B'H \cdot {S_{\Delta ABC}} = \frac{1}{2} \cdot B'H \cdot AB \cdot AC\).
Trong DAMN, ta có \[MN = AM \cdot \cot \widehat {ANM} = \frac{{a\sqrt 3 \cdot \cot \alpha }}{2}\].
Trong DABC, ta có
\(A{B^2} = BM \cdot BC \Rightarrow BM = \frac{{A{B^2}}}{{BC}} = \frac{{{a^2}}}{{2a}} = \frac{a}{2}\).Từ hai tam giác vuông đồng dạng là DBHB' và DBNM, ta có:
\(\frac{{B'H}}{{MN}} = \frac{{B'B}}{{MB}}\) Þ B'H = \(\frac{{MN \cdot B'B}}{{MB}}\) = \[\frac{{\frac{{a\sqrt 3 \cdot \cot \alpha }}{2} \cdot a}}{{\frac{a}{2}}}\] = \[a\sqrt 3 \cdot \cot \alpha \].
Vậy \({V_{ABC.A'B'C'}} = \frac{1}{2} \cdot B'H \cdot AB \cdot AC = \frac{1}{2} \cdot a\sqrt 3 \cdot \cot \alpha \cdot a \cdot a\sqrt 3 = \frac{3}{2}{a^3}\cot \alpha \). Chọn A.
Nhà sách vietjack
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Gọi \(I\) là tâm mặt cầu \(\left( S \right)\) thì độ dài đoạn \(OI\) đạt giá trị nhỏ nhất bằng
Xem đáp án »
25/04/2025
30
Câu 6:
Nếu GDP của Việt Nam năm 2023 là 500 tỷ USD, thì GDP của khu vực Nông - Lâm - Ngư nghiệp năm 2023 là bao nhiêu?
Xem đáp án »
25/04/2025
23
Câu 7:
Recent study has proven that there is no difference between the brain of the average woman and the average man.
Xem đáp án »
25/04/2025
22
🔥 Đề thi HOT:
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 1)
-
(2025) Đề thi thử Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG TP.HCM - Sử dụng ngôn ngữ Tiếng Việt - Chính tả
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 2)
-
(2025) Đề thi thử Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 2)
-
ĐGNL ĐHQG TP.HCM - Sử dụng ngôn ngữ Tiếng Việt - Tìm và phát hiện lỗi sai
-
(2025) Đề minh họa Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án ( Đề 8)
-
Đề thi Đánh giá năng lực ĐHQG Hồ Chí Minh năm 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận