Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng 2, \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\); góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(60^\circ \). Gọi \(M\) là trung điểm của cạnh \(AB\). Khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SCM} \right)\) là:
Câu hỏi trong đề: Đề thi ĐGNL ĐHQG Hồ Chí Minh (V-ACT) năm 2026-2027 (Đề 26) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
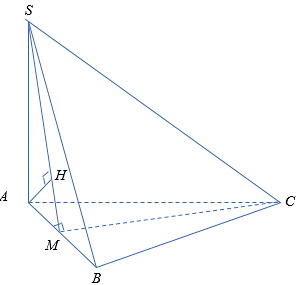
Vì \(AB\) là hình chiếu của \(SB\) trên mặt phẳng \(\left( {ABC} \right)\), nên góc giữa đường thẳng \(SB\) và mặt phẳng\(\left( {ABC} \right)\) bằng \[\widehat {SBA} = 60^\circ \]\[ \Rightarrow SA = AB \cdot tan60^\circ = 2\sqrt 3 \].
Do \[M = AB \cap \left( {SCM} \right)\], \(M\) là trung điểm của \(AB\)
\( \Rightarrow d\left( {A,\left( {SCM} \right)} \right) = d\left( {B,\left( {SCM} \right)} \right)\).
Vì \[\left\{ \begin{array}{l}CM \bot AB\\CM \bot SA\end{array} \right. \Rightarrow CM \bot \left( {SAB} \right)\].
Mặt khác \[CM \subset \left( {SCM} \right) \Rightarrow \left( {SCM} \right) \bot \left( {SAB} \right)\] và \[\left( {SCM} \right) \cap \left( {SAB} \right) = SM\], nên kẻ \[AH \bot SM\] tại \(H\)\[ \Rightarrow AH \bot \left( {SMC} \right)\]\( \Rightarrow AH = d\left( {A,\left( {SMC} \right)} \right) = d\left( {B,\left( {SMC} \right)} \right)\).Xét tam giác \(SAM\) vuông tại \(A\), ta có \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}} = \frac{1}{{{{\left( {2\sqrt 3 } \right)}^2}}} + \frac{1}{{{1^2}}} = \frac{{13}}{{12}}\)
\( \Rightarrow A{H^2} = \frac{{12}}{{13}} \Rightarrow AH = \sqrt {\frac{{12}}{{13}}} = \frac{{2\sqrt {39} }}{{13}}\).
Vậy khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {BCM} \right)\)bằng \(\frac{{2\sqrt {39} }}{{13}}\). Chọn C.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi A, B, C lần lượt là biến cố thí sinh được chọn lọt vào vòng sơ khảo, vòng bán kết và vòng chung kết.
Vì có 50% thí sinh lọt vào vòng sơ khảo nên \(P\left( A \right) = 0,5\).
Vì có 30% thí sinh của vòng sơ khảo được chọn để vào vòng bán kết nên \(P\left( {B|A} \right) = 0,3\).
Khi đó, xác suất để thí sinh lọt vào vòng bán kết là:
\(P\left( B \right) = P\left( {AB} \right) = P\left( {B|A} \right) \cdot P\left( A \right) = 0,3 \cdot 0,5 = 0,15\). Chọn B.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
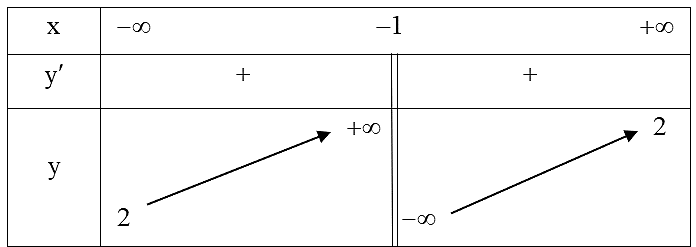
Nhìn đồ thị ta thấy đồ thị hàm số có đường tiệm cận xiên đi qua hai điểm \(M\left( { - 1\,;0} \right),N\left( {0\,;1} \right)\) nên có phương trình: \(y = x + 1\). Chọn A.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập