Cho biểu thức \(B = \frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + \frac{1}{{{7^2}}} + ... + \frac{1}{{{{100}^2}}}\). Chứng tỏ rằng \(\frac{1}{6} < B < \frac{1}{4}\)
Cho biểu thức \(B = \frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + \frac{1}{{{7^2}}} + ... + \frac{1}{{{{100}^2}}}\). Chứng tỏ rằng \(\frac{1}{6} < B < \frac{1}{4}\)
Quảng cáo
Trả lời:
Lời giải:
Ta có: \(\frac{1}{{{5^2}}} > \frac{1}{{5.6}};\,\,\,\frac{1}{{{6^2}}} > \frac{1}{{6.7}};\,\,....\,;\frac{1}{{{{100}^2}}} > \frac{1}{{100.101}}\)
\(\begin{array}{l}\frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}} > \frac{1}{{5.6}} + \frac{1}{{6.7}} + ... + \frac{1}{{100.101}}\\\frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}} > \frac{1}{5} - \frac{1}{6} + \frac{1}{6} - \frac{1}{7} + ... + \frac{1}{{100}} - \frac{1}{{101}}\\\frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}} > \frac{1}{5} - \frac{1}{{101}}\\\frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}} > \frac{{96}}{{505}} > \frac{1}{6}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\end{array}\)
Ta có: \(\frac{1}{{{5^2}}} < \frac{1}{{4.5}};\,\,\,\frac{1}{{{6^2}}} < \frac{1}{{5.6}};\,\,....\,;\frac{1}{{{{100}^2}}} < \frac{1}{{99.100}}\)
\(\begin{array}{l}\frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}} < \frac{1}{{4.5}} + \frac{1}{{5.6}} + ... + \frac{1}{{99.100}}\\\frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}} < \frac{1}{4} - \frac{1}{5} + \frac{1}{5} - \frac{1}{6} + ... + \frac{1}{{99}} - \frac{1}{{100}}\\\frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}} < \frac{1}{4} - \frac{1}{{100}}\\\frac{1}{{{5^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{100}^2}}} < \frac{6}{{25}} < \frac{1}{4}\,\,\,\,\,\,\,\,\,\,(2)\end{array}\)
Từ (1) và (2) suy ra \(\frac{1}{6} < B < \frac{1}{4}\) (đpcm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
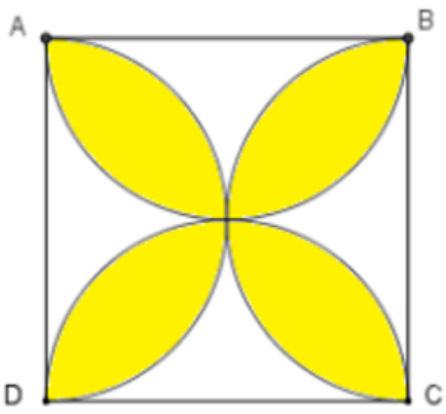
Xét parabol trên mặt phẳng Oxy có đỉnh I (0; 3) và cắt trục Ox tại hai điểm (-1; 0) và
(1; 0).
Khi đó phương trình của parabol là y = -3x2 + 3
Khi đó diện tích một cánh hoa là: \(\int\limits_{ - 1}^1 {\left| { - 3{x^2} + 3} \right|dx} \)= 4 (dm2)
Diện tích 1 hình lục giác đều cạnh bằng 2 dm là: \(6.\frac{{{2^2}\sqrt 3 }}{4} = 6\sqrt 3 \)
Khi đó diện tích của một hình là \(6\sqrt 2 + 6.4 = 24 + 6\sqrt 2 \) (dm2)
Diện tích của bức tường là: 3 ´ 4 = 12 (m2) = 1200 (dm2)
Bạn Hoa có thể vẽ tối đa số hình có cùng kích thước lên bức tường cần trang trí là:
\(\left[ {1200:(24 + 6\sqrt 2 } \right] = 34\)
Vậy bạn Hoa có thể vẽ tối đa 34 hình có cùng kích thước trên lên bức tường cần trang trí
Lời giải
Lời giải:
\[\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {4{x^2} + x} + 2x - 1} \right)\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{4{x^2} + x - {{(2x - 1)}^2}}}{{\sqrt {4{x^2} + x} - 2x + 1}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{4{x^2} + x - 4{x^2} + 4x - 1}}{{\sqrt {4{x^2} + x} - 2x + 1}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{5x}}{{ - x.\sqrt {4 + \frac{1}{x}} - 2x + 1}}\\ = \mathop {\lim }\limits_{x \to - \infty } \frac{{5 - \frac{1}{x}}}{{ - \sqrt {4 + \frac{1}{x}} - 2 + \frac{1}{x}}}\\ = \frac{{5 - 0}}{{ - \sqrt {4 + 0} - 2 + 0}} = \frac{5}{{ - 4}} = - \frac{5}{4}\end{array}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.