Câu hỏi:

19/08/2025 78

Cho tam giác ABC có CA = CB = 10 cm, AB = 12 cm. Kẻ CI ⊥ AB (I ∈ AB).

a) Chứng minh IA = IB .

b) Tính độ dài IC .

c) Kẻ IH ⊥ AC, IK ⊥ BC (H ∈ AC, K ∈ BC). Chứng minh IH = IK.

Xem lời giải

Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

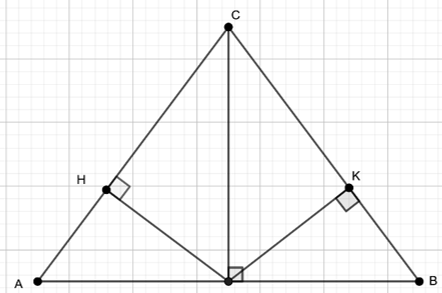
a) Ta có tam giác ABC có CA = CB nên tam giác ABC cân tại C.

Mà CI vuông góc AB nên IC là đường trung tuyến.

Vậy IB = IA.

b) Xét tam giác IBC vuông tại I, ta có

BC² = IC² + IB² ( định lý Pythagore)

Mà CB = 10 cm

IB = IA = \(\frac{1}{2}\)AB = \(\frac{1}{2}\). 12 = 6 (cm)

Nên 10² = IC² + 6²

IC² = 10² − 6² = 64

IC = 8 cm

c) Tam giác ABC cân tại C có IC là đường trung tuyến nên IC cũng là tia phân giác. Suy ra \(\widehat {ACI} = \widehat {ICB}\).

Xét hai tam giác vuông CIK và CIA, ta có

\(\widehat {ACI} = \widehat {ICB}\)
IC cạnh chung

Do đó ∆CIK = ∆CIH (cạnh huyền – góc nhọn)

Suy ra IH = IK (hai cạnh tương ứng)

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cô Lan phụ trách đội cần chia số trái cây trong đó 80 quả cam, 36 quả quýt và 104 quả mận vào các đĩa bánh kẹo trung thu sao cho số quả mỗi loại trong các đĩa là bằng nhau. Hỏi có thể chia thành nhiều nhất bao nhiêu đĩa, khi đó mỗi đĩa bao nhiêu trái cây loại?

Xem đáp án

Lời giải

Lời giải:

Gọi x là số đĩa hoa quả cần tìm

Theo đề bài, ta có

x ∈ ƯCLN(80, 36, 104)

80 = 2⁴ .5

36 = 2² .3²

104 = 2³ . 13

ƯCLN(80, 36, 104) = 2²= 4

Vậy có thể chia được 4 đĩa hoa quả

Mỗi đĩa có:

80 : 4 = 20 (quả cam)

36 : 4 = 9 (quả quýt)

104 : 4 = 26 (quả mận)

Đáp số: Mỗi đĩa có 20 quả cam, 9 quả quýt, 26 quả mận.

Câu 2

Có 20 viên bi gồm 3 loại: xanh, đỏ, vàng. Biết số bi xanh gấp 6 lần số bi đỏ, số bi vàng ít hơn số bi đỏ. Hỏi số bi vàng có bao nhiêu viên?

Xem đáp án

Lời giải

Lời giải:

Số bi đỏ gấp 6 lần số bi xanh, nên tổng của số bi đỏ và bi xanh phải là một số chia hết cho 7. Từ 1 đến 20 ta thấy chỉ có hai số chia hết cho 7 là: 7 và 14.

Nếu tổng số bi xanh và bi đỏ là 7 thì

Số bi vàng là:

20 – 7 = 13 (viên)

Vậy số bi vàng lớn hơn tổng số bi xanh với bi đỏ nên lớn hơn số bi đỏ suy ra trái với mệnh đề bài ra là số bi vàng ít hơn số bi đỏ.

Nếu tổng số bi xanh và bi đỏ là 14 thì

Số bi vàng là:

20 – 14 = 6 (viên)

Đáp số: 6 viên.

Câu 3