Câu hỏi:
11/05/2025 7
Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC).
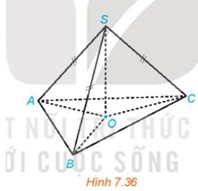
a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).
c) Chứng mình rằng nếu AO ⊥ BC thì SA ⊥ BC.
d) Xác định hình chiếu của tam giác SBC, SCA, SAB trên mặt phẳng (ABC).
Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC).
a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).
c) Chứng mình rằng nếu AO ⊥ BC thì SA ⊥ BC.
d) Xác định hình chiếu của tam giác SBC, SCA, SAB trên mặt phẳng (ABC).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
a) O là hình chiếu của S trên mặt phẳng (ABC) nên SO⊥ (ABC)
Mà OA, OB, OC ⊂ (ABC), suy ra SO ⊥ OA, SO ⊥ OB, SO ⊥ OC
Xét tam giác SAO vuông tại O (SO ⊥ OA) có
SA2 = OA2 + SO2 (Định lí Pytago)
Xét tam giác SBO vuông tại O (SO ⊥ OB) có
SB2 = OB2 + SO2 (Định lí Pytago)
Xét tam giác SCO vuông tại O (SO ⊥ OC) có
SC2 = OC2 + SO2 (Định lí Pytago)
Mà SA = SB = SC nên OA = OB = OC
Do đó O là tâm đường trọn ngoại tiếp tam giác ABC.
b) O là hình chiếu của S trên mặt phẳng (ABC)
A là hình chiếu của A trên mặt phẳng (ABC)
Suy ra OA là hình chiếu của SA trên mặt phẳng (ABC)
c) Ta có AO ⊥ BC, SO ⊥ BC (do SO ⊥ (ABC)), AO ∩ SO = {O}
Suy ra BC ⊥ (SAO); SA ⊂ (SAO)
Suy ra SA ⊥ BC.
d) O là hình chiếu của S trên mặt phẳng (ABC)
A là hình chiếu của A trên mặt phẳng (ABC)
B là hình chiếu của B trên mặt phẳng (ABC)
C là hình chiếu của C trên mặt phẳng (ABC)
Suy ra tam giác OAB là hình chiếu của tam giác SAB trên mặt phẳng (ABC)
Tam giác OBC là hình chiếu của tam giác SBC trên mặt phẳng (ABC)
Tam giác OCA là hình chiếu của tam giác SCA trên mặt phẳng (ABC).
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong các hình sau, hình nào không có tâm đối xứng?
A. Tam giác đều.
B. Hình chữ nhật.
C. Hình thoi.
D. Hình vuông.
Trong các hình sau, hình nào không có tâm đối xứng?
A. Tam giác đều.
B. Hình chữ nhật.
C. Hình thoi.
D. Hình vuông.
Xem đáp án »
11/05/2025
13
Câu 2:
Giữa một đám đất hình vuông có chu vi 60 m, người ta đào một cái giếng hình tròn, miệng giếng có đường kính 1,4 m. Xung quanh miệng giếng có xây một cái thành rộng 0,3 m.
a) Tính diện tích thành giếng.
b) Tính diện tích đất còn lại.
Giữa một đám đất hình vuông có chu vi 60 m, người ta đào một cái giếng hình tròn, miệng giếng có đường kính 1,4 m. Xung quanh miệng giếng có xây một cái thành rộng 0,3 m.
a) Tính diện tích thành giếng.
b) Tính diện tích đất còn lại.
Xem đáp án »
10/05/2025
11
Câu 7:
Một mảnh đất hình chữ nhật có chiều dài 28 m, chiều rộng 16 m và một mảnh đất hình vuông có chu vi 76 m. Hỏi chu vi mảnh đất hình chữ nhật nhiều hơn chu vi mảnh đất hình vuông bao nhiêu mét?
Một mảnh đất hình chữ nhật có chiều dài 28 m, chiều rộng 16 m và một mảnh đất hình vuông có chu vi 76 m. Hỏi chu vi mảnh đất hình chữ nhật nhiều hơn chu vi mảnh đất hình vuông bao nhiêu mét?
Xem đáp án »
10/05/2025
10
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận