Câu hỏi:
11/05/2025 64
Hình thang ABCD (AB // CD) có AB = AD + BC. Chứng minh rằng các tia phân giác của các góc C và D gặp nhau tại 1 điểm thuộc đáy AB.
Hình thang ABCD (AB // CD) có AB = AD + BC. Chứng minh rằng các tia phân giác của các góc C và D gặp nhau tại 1 điểm thuộc đáy AB.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
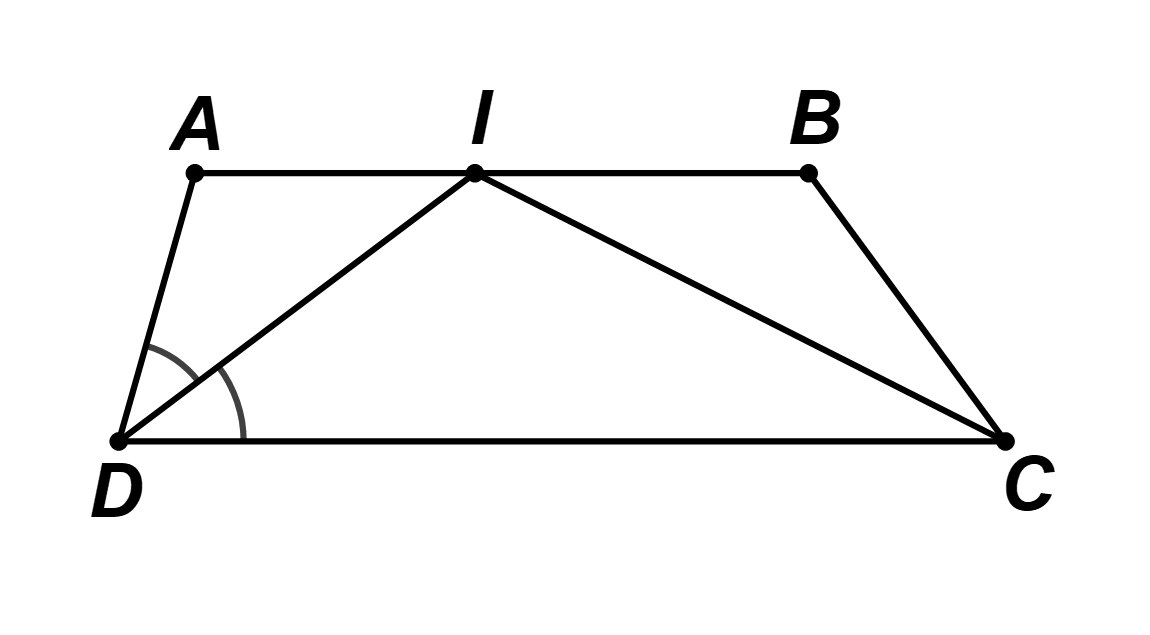
Gọi DI là phân giác của góc \[\widehat {ADC}\] (I thuộc AB) suy ra \(\widehat {ADI} = \widehat {CDI}\).
Vì AB // CD nên \(\widehat {CDI} = \widehat {AID}\) (so le trong)
Do đó \[\widehat {ADI} = \widehat {AID}\]
Xét ΔADI có \[\widehat {ADI} = \widehat {AID}\] nên ΔADI cân tại A
Suy ra AD = AI
Lại có AB = AD + BC và AB = AI + IB nên BI = BC
Do đó ΔBIC cân tại B, suy ra \[\widehat {BIC} = \widehat {BCI}\].
Do AB // CD nên \(\widehat {BIC} = \widehat {ICD}\) (so le trong)
Suy ra \[\widehat {BCI} = \widehat {ICD}\], do đó CI là phân giác của \[\widehat {DCB}.\]
Vậy các tia phân giác của các góc C và D gặp nhau tại điểm I thuộc đáy AB.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 5:
Đường kính của một bánh xe đạp là 0,65 m. Nếu bánh xe lăn trên mặt đất được 200 vòng thì xe đi được quãng đường dài bao nhiêu mét?
Đường kính của một bánh xe đạp là 0,65 m. Nếu bánh xe lăn trên mặt đất được 200 vòng thì xe đi được quãng đường dài bao nhiêu mét?
Xem đáp án »
10/05/2025
95
Câu 7:
Đường kính của một bánh xe đạp là 65 cm. Để người đi xe đạp được quãng đường 2041 m thì mỗi bánh xe phải lăn bao nhiêu vòng?
Đường kính của một bánh xe đạp là 65 cm. Để người đi xe đạp được quãng đường 2041 m thì mỗi bánh xe phải lăn bao nhiêu vòng?
Xem đáp án »
10/05/2025
86
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận