Cho hình vuông ABCD. Nối điểm chính giữa các cạnh của hình vuông ABCD ta được hình vuông EGTH. Nối điểm chính giữa các cạnh của hình vuông EGIH ta được hình vuông MNPQ (như hình vẽ). Tổng chu vi các tam giác hơn tổng chu vi các hình vuông có trong hình là chu vi của hình nào trong hình vẽ bên?
Cho hình vuông ABCD. Nối điểm chính giữa các cạnh của hình vuông ABCD ta được hình vuông EGTH. Nối điểm chính giữa các cạnh của hình vuông EGIH ta được hình vuông MNPQ (như hình vẽ). Tổng chu vi các tam giác hơn tổng chu vi các hình vuông có trong hình là chu vi của hình nào trong hình vẽ bên?
Câu hỏi trong đề: Đề thi ôn vào 6 môn Toán chất lượng cao có đáp án - Đề 6 !!
Quảng cáo
Trả lời:
Quan sát hình vẽ ta thấy:
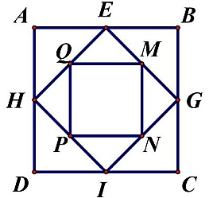
Tổng chu vi của các hình tam giác bằng tổng chu vi của: hình vuông ABCD + hình vuông MNPQ + 2 lần hình vuông EGIH.
Do đó tổng chu vi của các hình tam giác hơn tổng chu vi của các hình vuông có trong hình là chu vi của hình vuông EGIH.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
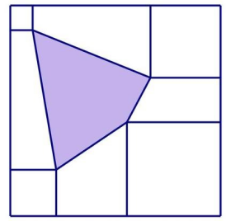
Theo chiều kim đồng hồ, độ dài cạnh của các hình vuông có diện tích 1cm2, 9cm2, 16cm2, 4cm2 lần lượt là 1cm, 3cm, 4cm, 2cm.
Độ dài cạnh của hình vuông lớn là: 9cm.
Ta đánh số như hình vẽ sau:
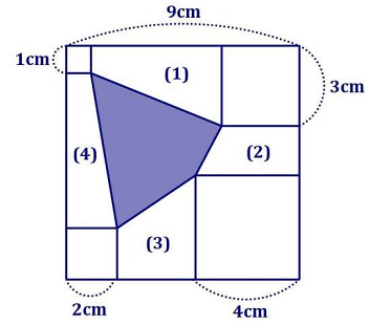
Quan sát hình vẽ, ta thấy các hình (1), (2), (3), (4) đều là hình thang vuông.
Chiều cao hình (1) là: 9 – 1 – 3 = 5 (cm)
Diện tích hình (1) là: (1 + 3) × 5 : 2 = 10 (cm2)
Chiều cao hình (2) là: 9 – 3 – 4 = 2(cm)
Diện tích hình (2) là: (3 + 4) × 2 : 2 = 7(cm2)
Chiều cao hình (3) là: 9 – 2 – 4 = 3 (cm)
Diện tích hình (3) là: (2 + 4) × 3 : 2 = 9 (cm2)
Chiều cao hình (4)là: 9 – 1 – 2 = 6 (cm)
Diện tích hình (4) là: (1 + 2) × 6 : 2 = 9(cm)
Diện tích hình tô đậm là: 81 – (10 + 7 + 9 + 9 + 1 + 9 + 16 + 4) = 16 (cm2)
Đáp số: 16 (cm2)
Lời giải
a) Giả sử hình vuông 4 × 4 được tô màu một số ô sao cho trong mỗi hình vuông 2 × 2 bất kì có đúng 2 ô được tô màu. Hình vuông 4 × 4 được chia thành 4 hình vuông 2 × 2 nên trong 16 ô vuông nhỏ có đúng 8 ô được tô màu.
Để số ô được tô màu trong hình vuông 3 × 3 là ít nhất thì phải tô nhiều ô nhất có thể ở 7 ô vuông nhỏ phía ngoài.
Đế ý rằng cột 2 và cột 4 số ô tô màu sẽ giống nhau, hàng 2 và hàng 4 số ô tô màu giống nhau, do đó ta có thể tô màu cho nhiều nhất 5 6 trong 7 ô phía ngoài.
Ví dụ ta tô như hình sau:

Vậy cần tô ít nhất: 8 – 5 = 3 (0) ở hình vuông 3 × 3 thoả mãn yêu cầu bài toán. Ví dụ ta tô màu như sau:

b) Giả sử hình vuông 8 × 8 được tô màu một số ô sao cho trong mỗi hình vuông 4 × 4 bất kì có đúng 5 ô được tô màu. Hình vuông 8 ×8 được chia thành 4 hình vuông 4 × 4 nên trong 64 ô vuông nhỏ có đúng 20 ô được tô màu.
Để số ô được tô màu trong hình vuông 7 × 7 là ít nhất thì phải tô nhiều ô nhất có thể ở 15 ô vuông nhỏ phía ngoài.
Đế ý rằng cột 4 và cột 8 số ô tô màu sẽ giống nhau, hàng 4 và hàng 8 số ô tô màu giống nhau, do đó ta có thể tô màu cho nhiều nhất 11 ô trong 15 ở phía ngoài.
Ví dụ ta tô màu như hình sau:

Vậy cần tô ít nhất: 20 – 11 = 9 (ô) ở hình vuông 7 × 7 thoả mãn yêu cầu bài toán.
Ví dụ ta tô màu như sau:

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.