Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh hình nón đó
A. tăng 4 lần.
B. giảm 4 lần.
C. tăng 2 lần.
D. không đổi.
Câu hỏi trong đề: Các dạng bài tập Hình trụ và hình nón lớp 9 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Ta có đường sinh mới là: \[{l_1} = \sqrt {{{\left( {2h} \right)}^2} + {{\left( {2r} \right)}^2}} = 2l\].
Khi đó, diện tích xung quanh mới là: π.(2R).(2l) = 4πrl.
Do đó, diện tích xung quanh của hình nón tăng lên 4 lần.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 18π (cm2).
B. 12 (cm2).
C. 12π (cm2).
D. 24π (cm2).
Lời giải
Đáp án đúng là: C
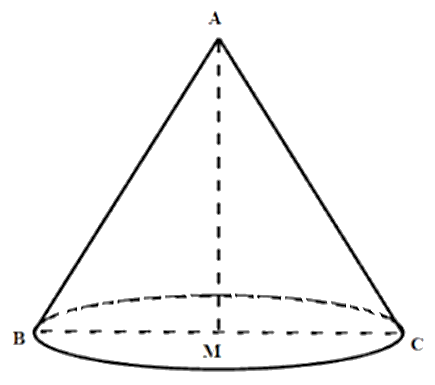
Xét tam giác ABC đều có AM vừa là đường cao vừa là đường trung tuyến.
Ta có: AM = \[2\sqrt 3 \] (cm).
Áp dụng định lí Pythagore, suy ra AM2 + MC2 = AC2 nên
l = AC = \[\sqrt {A{M^2} + M{C^2}} = \sqrt {12 + 4} = 4\] (cm).
Do đó, diện tích toàn phần của hình tạo thành là:
Stp = πr(l + r) = π. \[2.\left( {4 + 2} \right)\] = 12π (cm2).
Câu 2
Cho hình nón có đường kính đáy d = 18 cm và diện tích xung quanh 135π (cm2). Tính thể tích khối nón.
A. 972π (cm3).
B. 324π (cm3).
C. 324π (cm3).
D. 234π (cm3).
Lời giải
Đáp án đúng là: C
Bán kính đáy của hình nón là: 18 : 2 = 9 cm.
Đường sinh của hình nón là: 135π : 9π = 15 (cm).
Do đó, chiều cao của hình nón là: \[h = \sqrt {{{15}^2} - {9^2}} = 12\] cm.
Thể tích của khối nón là: \[\frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.9^2}.12. = 324\pi \] (cm3).
Câu 3
A. \[256\pi \sqrt {21} \] (cm3).
B. \[\frac{{24\pi \sqrt {21} }}{3}\] (cm3).
C. \[\frac{{256\pi }}{3}\](cm3).
D. \[\frac{{256\pi \sqrt {21} }}{3}\] (cm3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[\frac{{3\pi {a^2}}}{2}.\]
B. \[\frac{{3\pi {a^2}}}{4}.\]
C. \[\frac{{\pi {a^2}}}{2}.\]
D. \[\frac{{3{\pi ^2}a}}{2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 100π (cm3).
B. 120π (cm3).
C. 300π (cm3).
D. 200π (cm3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 25π (cm2).
B. 12π (cm2).
C. 20π (cm2).
D. 15π (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập