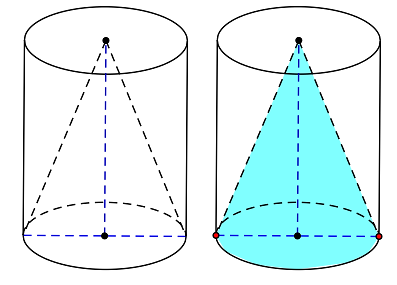
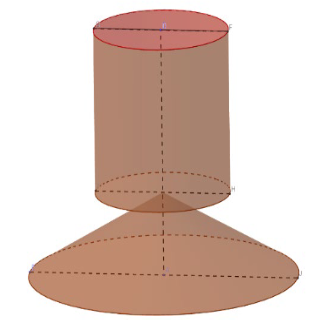
Cho một dụng cụ đựng chất lỏng được tạo bởi một hình trụ và hình nón được lặp đặt như hình bên. Bán kính đáy hình nón bằng bán kính đáy hình trụ. Chiều cao hình trụ bằng chiều cao hình nón và bằng h. Trong bình, lượng chất lỏng có chiều cao bằng \[\frac{1}{{24}}\] chiều cao hình trụ. Lật ngược dụng cụ theo phương vuông góc với mặt đất.

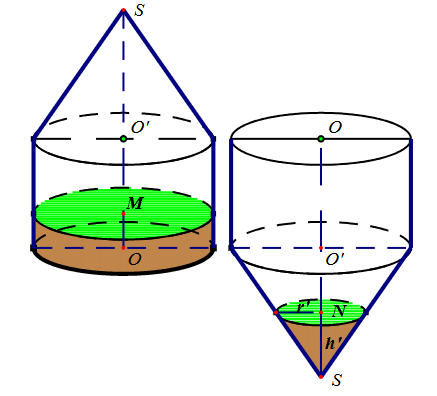
Tính độ cao phần chất lỏng trong hình nón theo h.

Đáp án đúng là: A

Nhận thấy hình nón có bán kính đáy và chiều cao bằng bán kính đáy và chiều cao của hình trụ.

Do đó, thể tích hình trụ là: V = πr²h.

Thể tích hình nón là: V₁ = \[\frac{1}{3}\]πr²h.

Suy ra thể tích phần gỗ bỏ đi là: V – V₁ = πr²h – \[\frac{1}{3}\]πr²h = \[\frac{2}{3}\]πr²h.

Mà thể tích phần còn lại là 640π cm³ và chiều cao là 15 cm.

Suy ra \[\frac{2}{3}\]πr².15 = 640π suy ra r = 8 (cm).

Độ dài đường sinh là: l = \[\sqrt {{h^2} + {r^2}} = \sqrt {{{15}^2} + {8^2}} = 17\]

Diện tích xung quanh của hình nón là: S_xq = πrl = 8.17.π = 136π (cm²).

Sử dụng dữ kiện của bài toán dưới đây để trả lời Câu 2, 3.

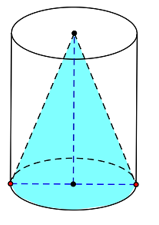
Từ một khúc gỗ hình trụ cao 24 cm, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là 960π cm³.

Đáp án đúng là: D

Nhận thấy hình nón có bán kính đáy và chiều cao bằng bán kính đáy và chiều cao của hình trụ.

Do đó, thể tích hình trụ là: V = πr²h.

Thể tích hình nón là: V₁ = \[\frac{1}{3}\]πr²h.

Suy ra thể tích phần gỗ bỏ đi là: V – V₁ = πr²h – \[\frac{1}{3}\]πr²h = \[\frac{2}{3}\]πr²h.

Mà thể tích phần còn lại là 960π cm³ và chiều cao là 24 cm.

Suy ra \[\frac{2}{3}\]πr².h = 960π hay πr².h = 960π : \[\frac{3}{2} = 1440\pi \] (cm³).