Cho tam giác ABC có diện tích bằng 90 cm2. Trên cạnh AC lấy điểm M sao cho AM = 2 MC. Lấy I là trung điểm của BM. Kéo dài AI cắt BC tại K.
a) Tính diện tích tam giác BMC.
b) Tính tỉ số diện tích hai tam giác ABI và BIC
c) So sánh
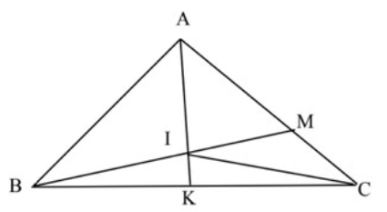
Cho tam giác ABC có diện tích bằng 90 cm2. Trên cạnh AC lấy điểm M sao cho AM = 2 MC. Lấy I là trung điểm của BM. Kéo dài AI cắt BC tại K.
a) Tính diện tích tam giác BMC.
b) Tính tỉ số diện tích hai tam giác ABI và BIC
c) So sánh
Câu hỏi trong đề: Đề thi vào lớp 6 môn Toán trường Nam Từ Liêm có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) (Chung đường cao hạ từ B và đáy MC = AC)
⇒ = 90 (
)
b) Nối IC ta có:
(Chung chiều cao hạ từ B và đấy AM = 2 x MC)
⇒ Chiều cao hạ từ A xuống BM gấp 2 lần chiều cao hạ từ C xuống đáy BM
⇒ (Chung đáy BI và chiều cao hạ từ A xuống BM gấp 2 lần chiều cao hạ từ C xuống đáy BM)
c) (Chung chiều cao hạ từ A và đáy BI = IM)
Mà (Chung đường cao hạ từ I và đáy AM = AC)
⇒
⇒ Đường cao hạ từ B xuống AI = đường cao từ C xuống AI
⇒ (Chung đáy AK và đường cao hạ từ B xuống AK = đường cao từ C xuống AK)
⇒ BK = CK
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Sau khi chuyển 3 quyển từ ngăn 1 sang ngăn 2 thì tổng số sách hai ngăn không đổi.
Số sách ngăn 2 lúc sau là:
48 : (3 + 5) x 5 = 30 (quyển)
Số sách ngăn 2 lúc đầu là:
30 – 3 = 27 (quyển)
Đáp số: 27 quyển
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) 2,4 x 150 + 8,6 x 240 – 24
= 24 x 15 + 86 x 24 – 24
= 24 x (15 + 86 – 1)
= 24 x 100
= 2 400
b)
c) Đổi giờ = giờ
Tổng vận tốc của an và Bình là:
= 27 (km/giờ)
Nếu Bình tăng vận tốc thêm 3 km mỗi giờ thì hai bạn sẽ gặp nhau ở chính giữa quãng đường nên vận tốc của An hơn vận tốc của Bình là 3 km/giờ.
Vận tốc của Bình là:
(27 – 3) : 2 = 12 (km/giờ)
Vận tốc của An là:
12 + 3 = 15 (km/giờ)
Đáp số: An: 15 km/giờ
Bình: 12km/giờ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập