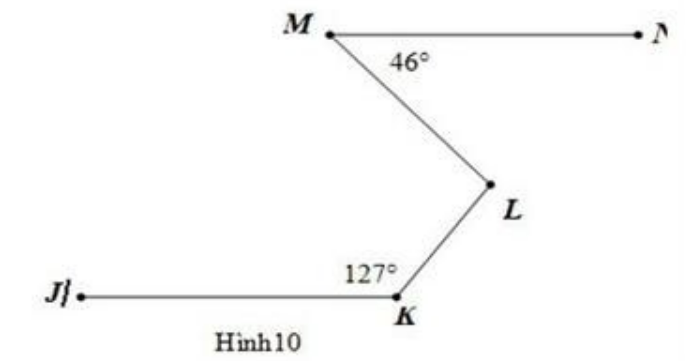
Tam giác ABC có góc A vuông, AB = 40 m, AC = 30 m; BC = 50 m. Trên AC lấy F, trên AB lấy E sao cho EFCB là hình thang có chiều cao là 12 m. Tính diện tích tam giác AFE và FEBC
Tam giác ABC có góc A vuông, AB = 40 m, AC = 30 m; BC = 50 m. Trên AC lấy F, trên AB lấy E sao cho EFCB là hình thang có chiều cao là 12 m. Tính diện tích tam giác AFE và FEBC
Quảng cáo
Trả lời:
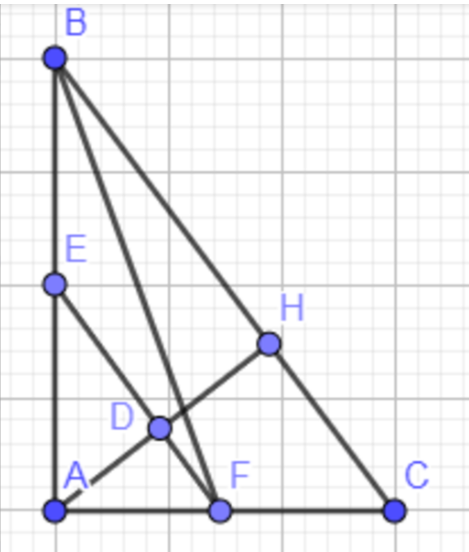
Diện tích tam giác ABC là: 40 ´ 30 : 2 = 600 (m2)
Diện tích tam giác FBC là: 12 ´ 50 : 2 = 300 (m2)
Diện tích tam giác AFB là: 600 – 300 = 300 (m2)
Kẻ đường cao AH ứng với đáy BC cắt EF tại D. Như vậy DH chính là đường cao của hình thang EFCB nên DH = 12 m.
Độ dài đoạn AH là: 600 ´ 2 : 50 = 24 (m)
Độ dài đoạn AD là: 24 – 12 = 12 (m)
Xét tam giác AEF và BFE có chung đáy EF, chiều cao AD = DH nên diện tích tam giác AEF = diện tích tam giác BEF và bằng \(\frac{1}{2}\) diện tích tam giác ABF.
Diện tích tam giác AEF là: 300 : 2 = 150 (m2)
Diện tích hình thang EFBC là: 600 – 150 = 450 (m2)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
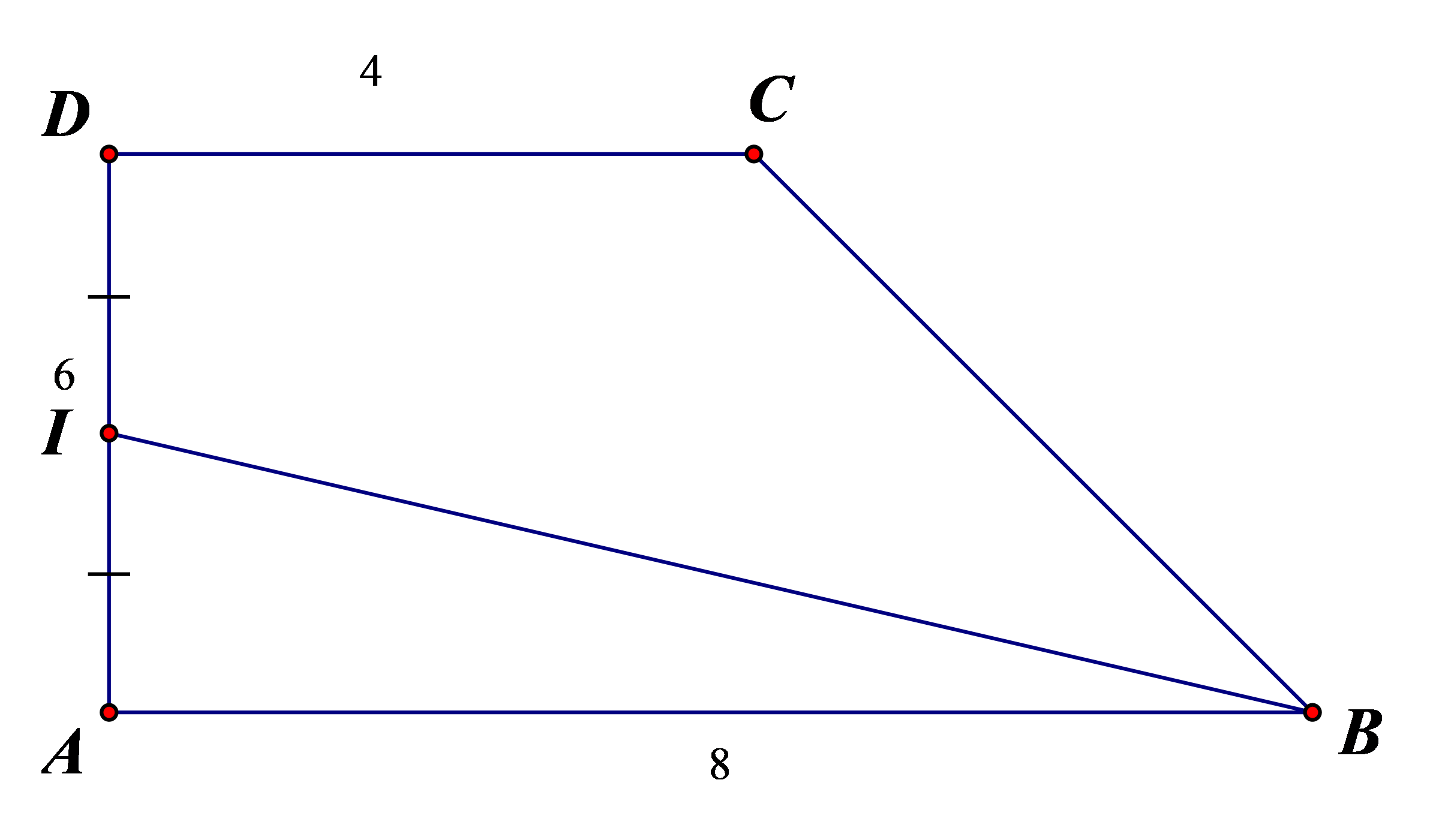
Vì I là trung điểm của AD Þ IA = ID = 3
Xét DIAB vuông tại A
\(\begin{array}{l}\tan \widehat {AIB} = \frac{8}{3} \Rightarrow \widehat {AIB} = 69,44^\circ \Rightarrow \widehat {DIB} = 110,56\\IB = \sqrt {I{A^2} + A{B^2}} = \sqrt {73} \end{array}\)
Ta có: \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} \)
\(\begin{array}{l} = \overrightarrow {IA} .\overrightarrow {ID} + \overrightarrow {IB} .\overrightarrow {ID} \\ = IA.ID.\cos \left( {IA,ID} \right) + IB.ID.\cos (IB,ID)\\ = - 3.3 + \sqrt {73} .3.\cos 110,56^\circ = - 18\end{array}\)
Lời giải
Lời giải:
Số tập con có một phần tử của X là: {4}, {5}
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.