Tìm các số tự nhiên n để phân số \(\frac{{3n + 2}}{{7n + 1}}\) là phân số tối giản

Xem lời giải

Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

Gọi ƯCLN (3n + 2, 7n + 1) = d (d là ước nguyên tố)

Ta có: \(\left\{ \begin{array}{l}3n + 2 \vdots d\\7n + 1 \vdots d\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}7\left( {3n + 2} \right) \vdots d\\3\left( {7n + 1} \right) \vdots d\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}21n + 14 \vdots d\\21n + 3 \vdots d\end{array} \right.\)

Nên \(\left( {21n + 14} \right) - \left( {21n + 3} \right) \vdots d \Rightarrow 11 \vdots d\)

Suy ra d Î {±1; ±11}

Do d là nguyên tố nên d = ±11

Do đó 3n + 2 \( \vdots \) 11

Khi đó 3n + 11 – 9 \( \vdots \) 11

Suy ra 3n \(\cancel{ \vdots }\)11

Do ƯC(3, 11) = 1 suy ra n \(\cancel{ \vdots }\)11

Để phân số tối giản thì n = 11k

Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình thang vuông ABCD có đáy lớn AB = 8; đáy nhỏ CD = 4; đường cao AD = 6; I là trung điểm của AD. Tính \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} \).

Xem đáp án

Lời giải

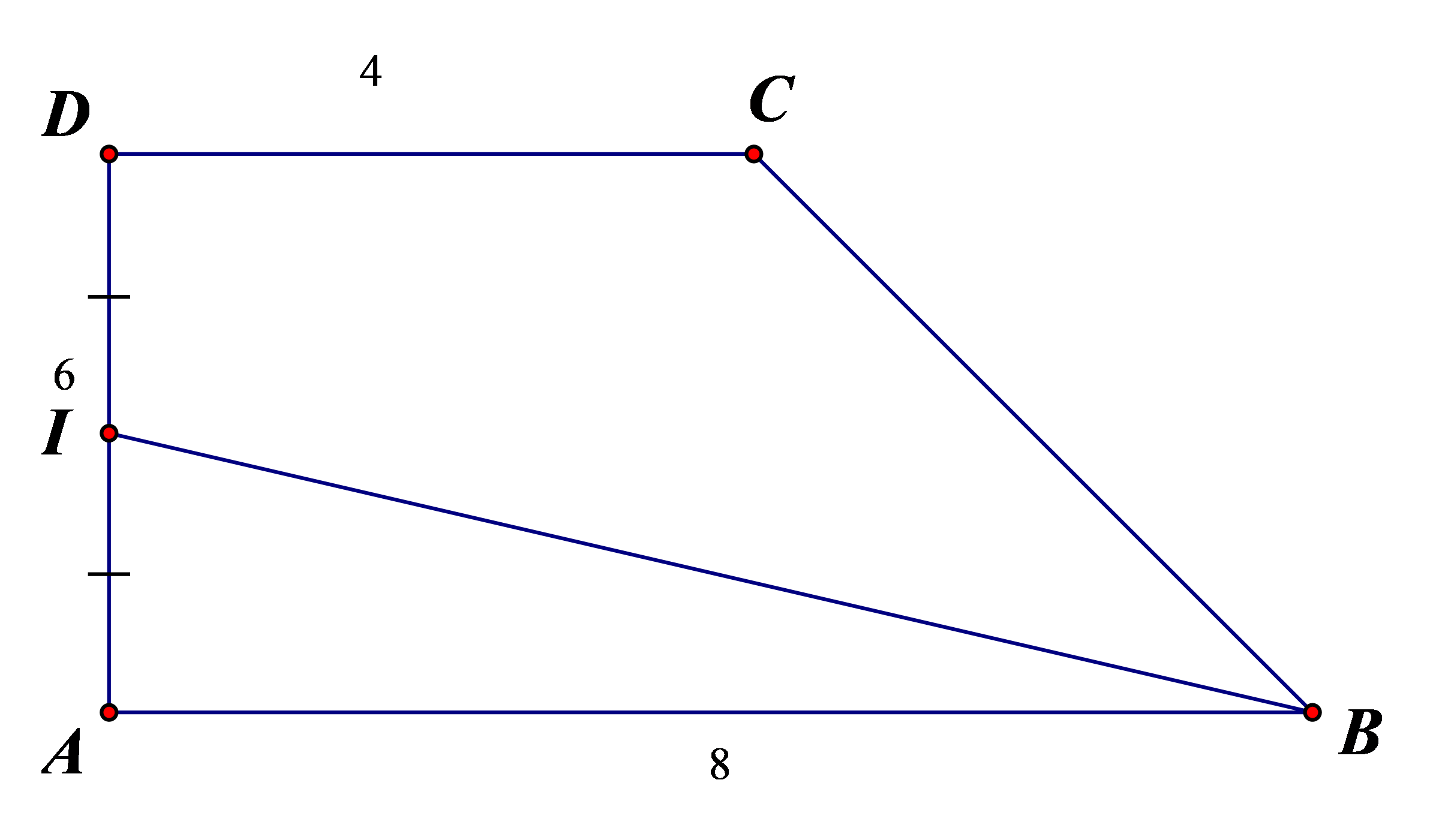
cho hình thang vuông abcd có đáy lớn ab=8a,đáy nhỏ cd=4a. (ảnh 1)

Vì I là trung điểm của AD Þ IA = ID = 3

Xét DIAB vuông tại A

\(\begin{array}{l}\tan \widehat {AIB} = \frac{8}{3} \Rightarrow \widehat {AIB} = 69,44^\circ \Rightarrow \widehat {DIB} = 110,56\\IB = \sqrt {I{A^2} + A{B^2}} = \sqrt {73} \end{array}\)

Ta có: \(\left( {\overrightarrow {IA} + \overrightarrow {IB} } \right).\overrightarrow {ID} \)

\(\begin{array}{l} = \overrightarrow {IA} .\overrightarrow {ID} + \overrightarrow {IB} .\overrightarrow {ID} \\ = IA.ID.\cos \left( {IA,ID} \right) + IB.ID.\cos (IB,ID)\\ = - 3.3 + \sqrt {73} .3.\cos 110,56^\circ = - 18\end{array}\)

Câu 2

Tìm a, b là các số nguyên dương sao cho a + b² chia hết cho a²b – 1.

Xem đáp án

Lời giải

Lời giải:

Theo đề bài: a + b² \( \vdots \) a²b – 1

Suy ra \(\exists k \in {\mathbb{N}^*}:\,\,a + {b^2} = k({a^2}b - 1)\) nên a + k = b(ka² – b)

Đặt m = ka² – b \(\left( {m \in \mathbb{Z}} \right)\) thì ta được a + k = mb

Mặt khác do a, k, b Î \({\mathbb{N}^*}\) nên cho ta m Î \({\mathbb{N}^*}\)

Từ đó ta có: (m – 1)(b – 1) = mb – m – b + 1 = a + k – ka² + 1 = (a + 1)(k – ka + 1)

Vì m, b Î \({\mathbb{N}^*}\) nên (m – 1)(b – 1) ³ 0

Do đó (a + 1)(k – ka + 1) ³ 0 nên 1 ³ k(a – 1).

Vì k, a Î \({\mathbb{N}^*}\) nên a – 1 ³ 0. Suy ra có 2 TH xảy ra:

TH1: k(a – 1) = 0 Þ a – 1 = 0 Û a = 1.

Thay a = 1 vào đẳng thức (m – 1)(b – 1) = (a + 1)(k – ka + 1) ta được:

(m – 1)(b – 1) = 2 Þ b – 1 = 1 hoặc b – 1 = 2 Þ b = 2 hoặc b = 3.

TH2: k(a – 1) = 1 Þ k = a – 1 = 1 hay k = 1 và a = 2.

Thay k = 1 và a = 2 vào đẳng thức (m – 1)(b – 1) = (a + 1)(k – ka + 1) ta được:

(m – 1)(b – 1) = 0 Þ m – 1 = 0 hoặc b - 1 = 0 Û m = 1 và b = 1

Nếu như m = 1 thì từ đẳng thức a + k = mb cho ta thấy b = 3.

Vậy có 4 cặp số nguyên dương (a, b) thỏa mãn yêu cầu bài toán là (1; 2); (1; 3); (2; 1); (2; 3)

Câu 3