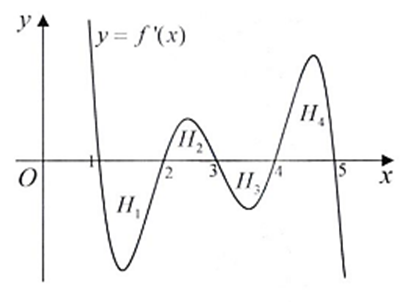
Trong không gian, cho (C) là đường tròn đường kính AB = 2R. Gọi (P) là mặt phẳng chứa (C). Cho S là điểm không thuộc (P) sao cho \[SA \bot \left( P \right)\]. Đặt SA = h. Giả sử M là một điểm di động trên (C) sao cho M khác A và B. Gọi H, K lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB, SM. Tìm điểm M trên (C) sao cho diện tích tam giác AHK lớn nhất và tính giá trị lớn nhất đó theo R và h.
Quảng cáo
Trả lời:
Giải bởi Vietjack
![Trong không gian, cho (C) là đường tròn đường kính AB = 2R. Gọi (P) là mặt phẳng chứa (C). Cho S là điểm không thuộc (P) sao cho \[SA \bot \left( P \right)\]. Đặt SA = h. Giả sử M là một điểm di động trên (C) sao cho M khác A và B. Gọi H, K lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB, SM. Tìm điểm M trên (C) sao cho diện tích tam giác AHK lớn nhất và tính giá trị lớn nhất đó theo R và h. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid6-1751015551.png)
Vì \(MB \bot MA\) và \(MB \bot SA\), suy ra \(MB \bot (SAM)\).
Do đó \(MB \bot AK\).
\(\left\{ {\begin{array}{*{20}{l}}{AK \bot SM}\\{AK \bot MB}\end{array}} \right. \Rightarrow AK \bot (SBM)\). Vì \(KH \subset (SBM)\), nên \(AK \bot KH\).\(\frac{1}{{A{H^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{4{R^2}}} \Rightarrow AH = \frac{{2Rh}}{{\sqrt {4{R^2} + {h^2}} }}\).
\({S_{AHK}} = \frac{{AK \cdot KH}}{2}\)
\( = \frac{{AK \cdot \sqrt {A{H^2} - A{K^2}} }}{2} \le \frac{{A{K^2} + (A{H^2} - A{K^2})}}{4} = \frac{{A{H^2}}}{4} = \frac{{{R^2}{h^2}}}{{4{R^2} + {h^2}}}\)Dấu "=" xảy ra khi và chỉ khi \(AK = \sqrt {A{H^2} - A{K^2}} \Leftrightarrow AK = \frac{{AH}}{{\sqrt 2 }}\).
Khi đó
\(\frac{1}{{A{M^2}}} = \frac{1}{{A{K^2}}} - \frac{1}{{{h^2}}} = \frac{2}{{A{H^2}}} - \frac{1}{{{h^2}}} = 2\left( {\frac{1}{{{h^2}}} + \frac{1}{{4{R^2}}}} \right) - \frac{1}{{{h^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{2{R^2}}}\).
Suy ra \(AM = \frac{{\sqrt 2 Rh}}{{\sqrt {2{R^2} + {h^2}} }}\).Kiểm tra trực tiếp ta có \(0 < AM = \frac{{\sqrt 2 Rh}}{{\sqrt {2{R^2} + {h^2}} }} < 2R\).
Vì thế M là giao điểm của đường tròn (C) và đường tròn tâm A, bán kính \(\frac{{\sqrt 2 Rh}}{{\sqrt {2{R^2} + {h^2}} }}\).
Giá trị lớn nhất của \({S_{AHK}}\) là \(\frac{{{R^2}{h^2}}}{{4{R^2} + {h^2}}}\) khi \(AM = \frac{{\sqrt 2 Rh}}{{\sqrt {2{R^2} + {h^2}} }}\).Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
C. 5.
![Hình vẽ bên minh hoạ mặt cắt đứng của một con kênh đặt trong hệ trục tọa độ Oxy. Biết rằng đường cong AOB của mặt cắt là một phần của đồ thị hàm số \[f\left( x \right) = \frac{3}{{100}}\left( { - \frac{1}{3}{x^3} + 5{x^2}} \right)\]. Hãy tính diện tích hình phẳng được tô màu đậm, biết đơn vị trên mỗi trục tọa độ là mét. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid5-1751015527.png)
Lời giải
Ta có: \(5 = \frac{3}{{100}}( - \frac{1}{3}{x^3} + 5{x^2}) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 5}\\{x = 10}\end{array}} \right.\). Suy ra \(A( - 5;5)\).
Diện tích của hình phẳng được tô màu đậm bằng:
\(S = \int_{ - 5}^{10} {\left[ {5 - \frac{3}{{100}}( - \frac{1}{3}{x^3} + 5{x^2})} \right]} dx\)\(S = \int_{ - 5}^{10} {( - \frac{1}{{100}}{x^3} - \frac{3}{{20}}{x^2} + 5)} dx = \left[ { - \frac{1}{{100}}\frac{{{x^4}}}{4} - \frac{3}{{20}}\frac{{{x^3}}}{3} + 5x} \right]|_{ - 5}^{10}\)
Vậy \(S = \frac{{675}}{{16}}({m^2}) = 42,1875({m^2})\).
Câu 3
A. 56.
B. -2.
C. 3.
D. 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(a{b^2} = 0\).
B. \(a{b^2} = - 3\).
C. \(a{b^2} < - 4\).
D. \(a{b^2} > - 3\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(y = \frac{{2x - 3}}{{2x + 2}}\)
B. \(y = \frac{{x - 3}}{{x + 2}}\)
C. \(y = \frac{{x - 3}}{{2x - 4}}\)
D. \(y = \frac{{x - 3}}{{x - 2}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{{{a^3}}}{{24}}\)
B. \(\frac{{{a^3}}}{4}\)
C. \(\frac{{{a^3}}}{{12}}\)
D. \(\frac{{{a^3}}}{6}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo