(1,0 điểm) Bạn An mua \(3\) quyển sách có giá niêm yết là \(80\) nghìn đồng/quyển và \(18\) quyển vở có giá niêm yết là \(14\) nghìn đồng/quyển. Bạn An dùng thẻ tín dụng thanh toán cho cửa hàng để được hoàn tiền 10% giá trị hóa đơn. Hỏi số tiền thực tế bạn An phải trả là bao nhiêu nếu số tiền hoàn ngay sau khi quẹt thẻ?

Hướng dẫn giải

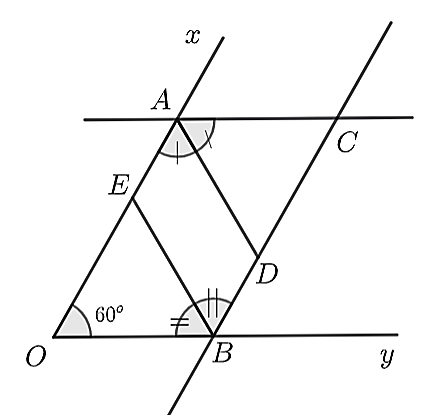
a) Ta có: \(Oy\parallel AC\) nên \(\widehat {xAC} = \widehat {xOy} = 60^\circ \) (đồng vị).

Mà \(\widehat {OAC}\) và \(\widehat {xAC}\) là hai góc kề bù nên \(\widehat {OAC} + \widehat {xAC} = 180^\circ \).

Do đó, \(\widehat {OAC} = 180^\circ - \widehat {xAC} = 180^\circ - 60^\circ = 120^\circ \).

Lại có \(AD\) là phân giác của \(\widehat {OAC}\) nên \(\widehat {OAD} = \widehat {DAC} = \frac{{\widehat {OAC}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \).

Lại có \(Ox\parallel BC\) nên \(\widehat {ADC} = \widehat {OAD} = 60^\circ \) (so le trong)

Vậy \(\widehat {ADC} = 60^\circ \).

b) Ta có \(Ox\parallel BC\) nên \(\widehat {yBC} = \widehat {yOx} = 60^\circ \) (đồng vị);

Mà \(\widehat {CBy}\) và \(\widehat {CBO}\) là hai góc kề bù nên \(\widehat {CBy} + \widehat {CBO} = 180^\circ \).

Suy ra \[\widehat {CBO} = 180^\circ - \widehat {CBy} = 180^\circ - 60^\circ = 120^\circ \].

Lại có \(BE\) là tia phân giác của \(\widehat {CBO}\) nên \(\widehat {CBE} = \widehat {EBO} = \frac{{\widehat {OBC}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \).

Khi đó, \(\widehat {CBE} = \widehat {ADC} = 60^\circ \).

Mà hai góc ở vị trí đồng vị nên \(AD\parallel BE.\)

Hướng dẫn giải

Đáp án đúng là: \(0,75\).

Ta có: \(\frac{1}{2} - \frac{1}{2}{\left( {2x - 1} \right)^2} = \frac{3}{8}\)

\(\frac{1}{2}{\left( {2x - 1} \right)^2} = \frac{1}{2} - \frac{3}{8}\)

\(\frac{1}{2}{\left( {2x - 1} \right)^2} = \frac{1}{8}\)

\({\left( {2x - 1} \right)^2} = \frac{1}{8}:\frac{1}{2}\)

\({\left( {2x - 1} \right)^2} = \frac{1}{4}\)

\({\left( {2x - 1} \right)^2} = {\left( {\frac{1}{2}} \right)^2} = {\left( { - \frac{1}{2}} \right)^2}\) .

Suy ra \(2x - 1 = \frac{1}{2}\) hoặc \(2x - 1 = - \frac{1}{2}\)

Do đó \(2x = \frac{3}{2}\) hoặc \(2x = \frac{1}{2}\).

Nên \(x = \frac{3}{4}\) hoặc \(x = \frac{1}{4}\)

Hay \(x = 0,75\) hoặc \(x = 0,25\).

Mà \(x > \frac{1}{2}\) hay \(x > 0,5\) nên \(x = 0,75.\)

Vậy \(x = 0,75.\)