(1,0 điểm) Bác Kiên tiết kiệm được \(3{\rm{ 150 000}}\) đồng và dự định mua \(20\) phần quà gửi tặng đồng bào miền Bắc sau đợt bão Yagi. Mỗi phần quà gồm một thùng mì có giá \(106{\rm{ 000}}\) đồng và \(5{\rm{ kg}}\) gạo có giá \(20{\rm{ 000}}\) đồng/kg. Khi đi mua hàng, bác Kiên được giảm giá \(5\% \) cho mỗi thùng mì. Hỏi với số tiền tiết kiệm trên, bác Kiên có thực hiện được dự định của mình không?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Số tiền mua \(5{\rm{ kg}}\) gạo là: \(20{\rm{ }}000.5 = 100{\rm{ }}000\) (đồng).
Số tiền dự định mua 20 thùng mì tôm là: \(20.106{\rm{ }}000 = 2{\rm{ }}120{\rm{ }}000\) (đồng)
Số tiền được giảm khi mua 20 thùng mì tôm là: \(2{\rm{ }}120{\rm{ }}000.5\% = 106{\rm{ }}000\) (đồng).
Do đó, số tiền thực tế khi mua 20 thùng mì tôm là: \(2{\rm{ }}120{\rm{ }}000 - 106{\rm{ }}000 = 2{\rm{ }}014{\rm{ }}000\) (đồng).
Số tiền khi mua 20 phần gạo là: \(20.100{\rm{ }}000 = 2{\rm{ }}000{\rm{ }}000\) (đồng).
Suy ra số tiền mua 20 phần quà là: \(2{\rm{ }}014{\rm{ }}000 + 2{\rm{ }}000{\rm{ }}000 = 4{\rm{ }}014{\rm{ }}000\) (đồng).
Nhận thấy \(4{\rm{ }}014{\rm{ }}000 > 3{\rm{ }}150{\rm{ }}000\) nên với số tiền tiết kiệm trên, bác Kiên chưa thực hiện được dự định của mình.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a)
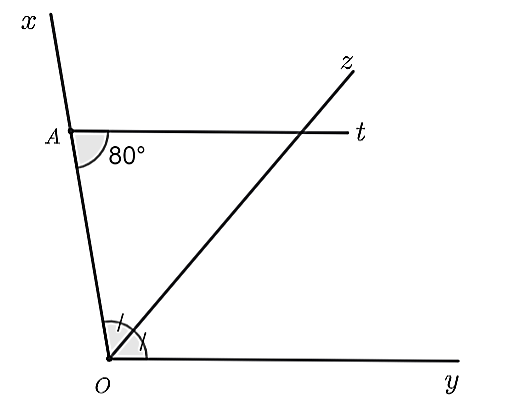
Ta có \(\widehat {OAt}\) và \(\widehat {xAt}\) là hai góc kề bù, do đó \(\widehat {OAt} + \widehat {xAt} = 180^\circ \).
Do đó, \(\widehat {xAt} = 180^\circ - \widehat {OAt} = 180^\circ - 80^\circ = 100^\circ \).
Vậy \(\widehat {xAt} = 100^\circ .\)
b)
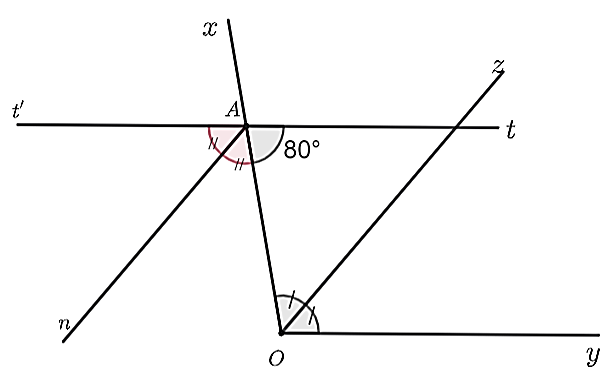
Nhận thấy \(\widehat {xAt} = \widehat {xOy} = 100^\circ \), mà hai góc ở vị trí đồng vị nên \(At\parallel Oy\).
Có \(\widehat {t'AO} = \widehat {xAt} = 100^\circ \) (hai góc đối đỉnh).
Vì \(An\) là tia phân giác của \(\widehat {OAt'}\) nên ta có \(\widehat {t'An} = \widehat {nAO} = \frac{{\widehat {t'AO}}}{2} = \frac{{100^\circ }}{2} = 50^\circ \).
Lại có \(Oz\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{{\widehat {xOy}}}{2} = \frac{{100^\circ }}{2} = 50^\circ \).
Do đó, \(\widehat {OAn} = \widehat {AOz} = 50^\circ \).
Mà hai góc ở vị trí so le trong nên \(An\parallel Oz\).
Lời giải
Hướng dẫn giải
|
a) \(\frac{5}{6} + \frac{2}{3} - 0,5\) \( = \frac{5}{6} + \frac{4}{6} - \frac{1}{2}\) \( = \frac{9}{6} - \frac{3}{6}\) \( = \frac{6}{6}\) \( = 1\). |
b) \( - \sqrt {\frac{4}{{49}}} \cdot \left( {\frac{5}{{13}} - \frac{9}{{15}}} \right) - \frac{2}{7} \cdot \sqrt {{{\left( {\frac{{ - 8}}{{13}}} \right)}^2}} \) \[ = - \sqrt {{{\left( {\frac{2}{7}} \right)}^2}} \cdot \left( {\frac{5}{{13}} - \frac{9}{{15}}} \right) - \frac{2}{7} \cdot \left| {\frac{{ - 8}}{{13}}} \right|\] \( = - \frac{2}{7} \cdot \left( {\frac{5}{{13}} - \frac{9}{{15}}} \right) - \frac{2}{7} \cdot \frac{8}{{13}}\) \( = - \frac{2}{7} \cdot \left( {\frac{5}{{13}} - \frac{9}{{15}} + \frac{8}{{13}}} \right)\) \( = - \frac{2}{7} \cdot \left( {\frac{5}{{13}} + \frac{8}{{13}} - \frac{9}{{15}}} \right)\) \( = - \frac{2}{7} \cdot \left( {\frac{{13}}{{13}} - \frac{9}{{15}}} \right)\)\( = - \frac{2}{7} \cdot \left( {1 - \frac{9}{{15}}} \right)\) \( = - \frac{2}{7} \cdot \frac{6}{{15}} = \frac{{ - 4}}{{35}}.\) |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(a - b + c + d = 0.\)
B. \(a = b + c + d.\)
C. \(b = d - a - c.\)
D. \(c = b - a + d.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Thu Nga Trần Thị
Trả lời ngắn hơn so với cái ở trên