Cho các số sau: \(3,75;{\rm{ }}\frac{6}{5};{\rm{ }} - 5\pi ;{\rm{ }}\sqrt 7 ;{\rm{ }}\sqrt 2 + 2;{\rm{ }}\sqrt {25} ;{\rm{ 0,1232323}}....{\rm{; }}\frac{2}{3}.\) Trong các số trên, có bao nhiêu số là số vô tỉ?
Câu hỏi trong đề: Bộ 3 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: \(3\).
Nhận thấy:
• Các số \(3,75;{\rm{ }}\frac{6}{5};{\rm{ }}\frac{2}{3}\) là các số hữu tỉ.
• \(\sqrt {25} = \sqrt {{5^2}} = 5\) là số hữu tỉ.
• \({\rm{0,1232323}}.... = 0,{\rm{1}}\left( {23} \right)\) là số thập phân vô hạn tuần hoàn.
• Các số vô tỉ trong các số trên là \( - 5\pi ;{\rm{ }}\sqrt 7 ;{\rm{ }}\sqrt 2 + 2\).
Do đó, có 3 số vô tỉ trong các số trên.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a)
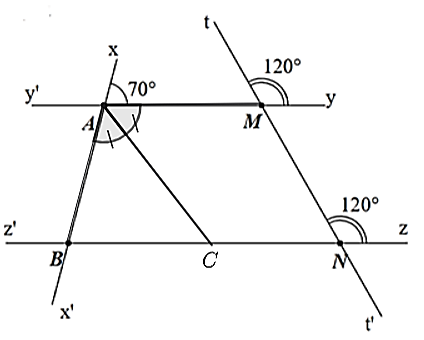
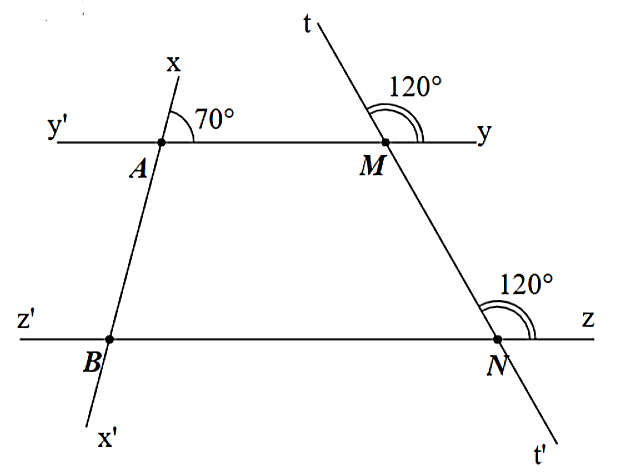
Ta có: \(\widehat {tMy} = \widehat {tNz} = 120^\circ \) và hai góc ở vị trí đồng vị nên \(yy'\parallel zz'\).
Suy ra \(\widehat {ABN} = \widehat {xAM} = 70^\circ \) (hai góc đồng vị).
Vì \(\widehat {BAM}\) và \(\widehat {xAM}\) là hai góc kề bù nên \(\widehat {BAM} + \widehat {xAM} = 180^\circ \)
Do đó \(\widehat {BAM} = 180^\circ - \widehat {xAM} = 180^\circ - 70^\circ = 110^\circ \).
Ta có \(AC\) là phân giác của \(\widehat {BAM}\) nên \(\widehat {BAC} = \widehat {CAM} = \frac{{\widehat {BAM}}}{2} = \frac{{110^\circ }}{2} = 55^\circ .\)
Vì \(yy'\parallel zz'\) nên \(\widehat {ACB} = \widehat {MAC} = 55^\circ \) (so le trong).
Lại có \(\widehat {ACB}\) và \(\widehat {ACN}\) là hai góc kề bù nên \(\widehat {ACN} + \widehat {ACB} = 180^\circ \)
Suy ra \(\widehat {ACN} = 180^\circ - \widehat {ACB} = 180^\circ - 55^\circ = 125^\circ \).
b)
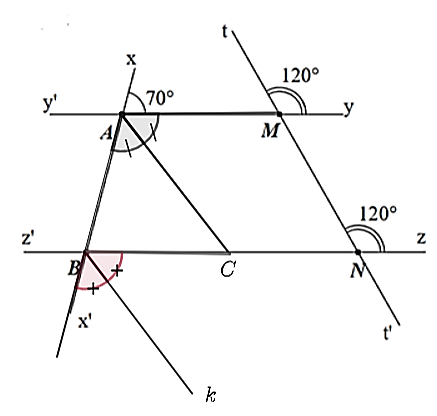
Ta có \(\widehat {ABN}\) và \(\widehat {x'BN}\) là hai góc kề bù nên \(\widehat {ABN} + \widehat {x'BN} = 180^\circ \)
Suy ra \[\widehat {x'BN} = 180^\circ - \widehat {ABN} = 180^\circ - 70^\circ = 110^\circ \].
Mà \(Bk\) là tia phân giác của \(\widehat {x'BN}\) nên \(\widehat {x'Bk} = \widehat {kBC} = \frac{{110^\circ }}{2} = 55^\circ \).
Ta có \(\widehat {x'Bk} = \widehat {BAC} = 55^\circ \) và hai góc ở vị trí đồng vị nên \(AC\parallel Bk.\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng.b) Đúng.c) Đúng.d) Sai.
• Số học sinh Xuất sắc và Giỏi so với số học sinh cả lớp là \(1 - \frac{9}{{16}} = \frac{7}{{16}}\) (số học sinh).
Do đó, ý a) là đúng.
• Số học sinh Khá lớp 7A là: \(\frac{9}{{16}}.48 = 27\) (học sinh). Do đó, ý b) đúng.
• Số học sinh Giỏi và Xuất sắc của lớp 7A là: \(48 - 27 = 21\) (học sinh). Do đó, ý c) đúng.
• Ta có số học sinh Giỏi bằng \(\frac{{11}}{{10}}\) số học sinh Xuất sắc nên ta có số học sinh Giỏi là:
\(21:\left( {11 + 10} \right).11 = 11\) (học sinh).
Số học sinh Xuất sắc là: \(21 - 11 = 10\) (học sinh). Do đó, ý d) là sai.
Câu 3
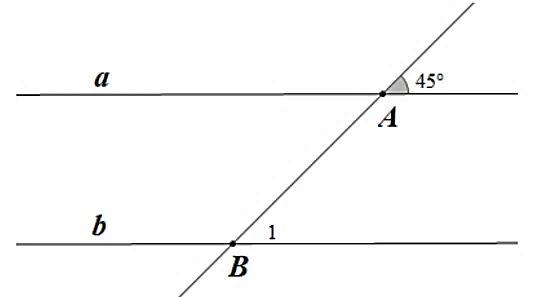
A. \(135^\circ .\)
B. \(35^\circ .\)
C. \(45^\circ .\)
D. \(145^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[x - \frac{1}{5} = \frac{3}{5}\].
B. \[x - \frac{1}{2} = \frac{3}{5}:\frac{2}{5}\].
C. \[x - \frac{2}{5} = \frac{3}{5} + \frac{1}{2}\].
D. \[x - \frac{1}{2} = \frac{3}{5} + \frac{2}{5}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
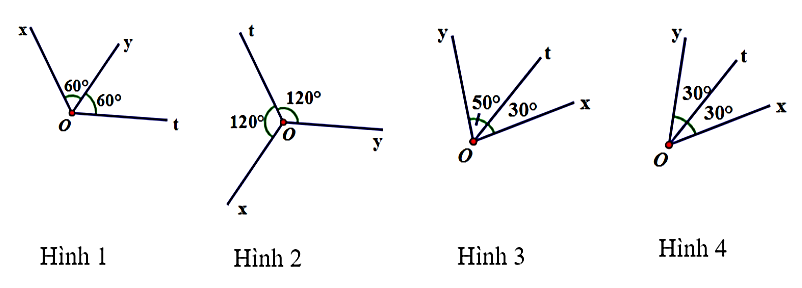
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.