A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Số nào trong các số dưới đây không là số hữu tỉ?
A. \(\frac{3}{0}.\)
B. \(0,625.\)
C. \(\frac{0}{3}.\)
D. \(3\frac{2}{5}.\)
Câu hỏi trong đề: Bộ 2 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Số hữu tỉ là số viết được dưới dạng \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).
Do đó, \(\frac{3}{0}\) không là số hữu tỉ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
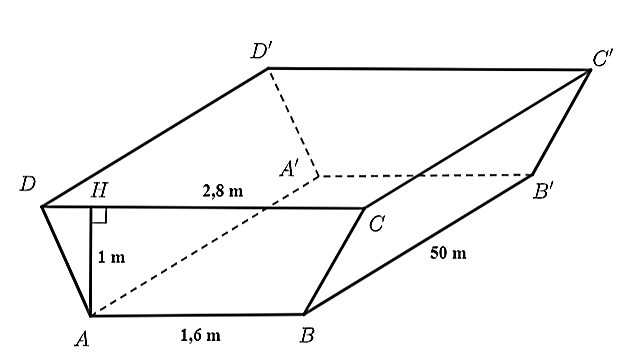
Thể tích khối đất phải đào để làm đoạn mương đó là: \(\frac{{\left( {1,6 + 2,8} \right) \cdot 1}}{2} \cdot 50 = 110\) (m3).
Số tiền công phải trả để đào được đoạn mương đó là: \(240{\rm{ }}000 \cdot 110 = 26{\rm{ }}400{\rm{ }}000\) (đồng).
Lời giải
Hướng dẫn giải
Ta có: \(5A = 1 + \frac{2}{5} + \frac{3}{{{5^2}}} + \frac{4}{{{5^3}}} + ... + \frac{{1\,\,000}}{{{5^{999}}}}.\)
Suy ra \(5A - A = \left( {1 + \frac{2}{5} + \frac{3}{{{5^2}}} + \frac{4}{{{5^3}}} + ... + \frac{{1\,\,000}}{{{5^{999}}}}} \right) - \left( {\frac{1}{5} + \frac{2}{{{5^2}}} + \frac{3}{{{5^3}}} + \frac{4}{{{5^4}}} + ... + \frac{{1\,\,000}}{{{5^{1\,\,000}}}}} \right)\)
\(4A = 1 + \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{999}}}} - \frac{{1\,\,000}}{{{5^{1\,\,000}}}}.\)
Đặt \(B = \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{999}}}}\).
Ta có \(5B = 1 + \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{998}}}}.\)
Suy ra \(5B - B = \left( {1 + \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{998}}}}} \right) - \left( {\frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{999}}}}} \right)\)
\(4B = 1 - \frac{1}{{{5^{999}}}}\) nên \(B = \frac{1}{4} \cdot \left( {1 - \frac{1}{{{5^{999}}}}} \right)\).
Do đó, \(4A = 1 + \frac{1}{4} \cdot \left( {1 - \frac{1}{{{5^{999}}}}} \right) - \frac{{1\,\,000}}{{{5^{1\,\,000}}}} = \frac{5}{4} - \frac{1}{4} \cdot \frac{1}{{{5^{999}}}} - \frac{{1\,\,000}}{{{5^{1\,\,000}}}}.\)
Khi đó, \(A = \frac{5}{{16}} - \frac{1}{{16}} \cdot \frac{1}{{{5^{999}}}} - \frac{{250}}{{{5^{1\,\,000}}}} < \frac{5}{{16}}.\)
Vậy \(A < \frac{5}{{16}}\).
Câu 3
A. \(3.\)
B. \(\frac{3}{5}.\)
C. \(\frac{5}{3}.\)
D. \(\frac{2}{5}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(a + 2b - c.\)
B. \(a + 2b + c.\)
C. \(a - c.\)
D. \(a + c.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.