Có bao nhiêu kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu?
A. \(1.\)
Quảng cáo
Trả lời:
Đáp án đúng là: B
Có hai kết quả có thể xảy ra của phép thử tung một đồng xu đó là: xuất hiện mặt sấp (S) hoặc xuất hiện mặt ngửa (N).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
3.1. Số lần lấy một chiếc bút là: \(n = 50.\)
Số lần lấy được bút màu đỏ là: \(k = 50 - 20 = 30\) (lần)
Xác suất thực nghiệm của sự kiện “lấy được bút màu đỏ” là: \(\frac{k}{n} = \frac{{30}}{{50}} = \frac{3}{5}.\)
3.2. Ta có:
\(M = \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6} - \frac{1}{7} + \frac{1}{8} - \frac{1}{9} + ... + \frac{1}{{2022}} - \frac{1}{{2023}}\)
\(M = \left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5}} \right) + \left( {\frac{1}{6} - \frac{1}{7}} \right) + \left( {\frac{1}{8} - \frac{1}{9}} \right) + ... + \left( {\frac{1}{{2022}} - \frac{1}{{2023}}} \right)\)
\(M = \frac{{13}}{{60}} + \left( {\frac{1}{6} - \frac{1}{7}} \right) + \left( {\frac{1}{8} - \frac{1}{9}} \right) + ... + \left( {\frac{1}{{2022}} - \frac{1}{{2023}}} \right)\)
Nhận thấy \(\frac{{13}}{{60}} > \frac{{12}}{{60}}\)
Do đó, \(\frac{{13}}{{60}} + \left( {\frac{1}{6} - \frac{1}{7}} \right) + \left( {\frac{1}{8} - \frac{1}{9}} \right) + ... + \left( {\frac{1}{{2022}} - \frac{1}{{2023}}} \right) > \frac{{12}}{{60}}\) hay \(M > \frac{{12}}{{60}}\).
Suy ra \(M > \frac{1}{5}\) (1).
Lại có: \(M = \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6} - \frac{1}{7} + \frac{1}{8} - \frac{1}{9} + ... + \frac{1}{{2022}} - \frac{1}{{2023}}\)
\(M = \left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6}} \right) - \left( {\frac{1}{7} - \frac{1}{8}} \right) - \left( {\frac{1}{9} - \frac{1}{{10}}} \right) - ... - \left( {\frac{1}{{2021}} - \frac{1}{{2022}}} \right) - \frac{1}{{2023}}\)
\(M = \frac{{23}}{{60}} - \left( {\frac{1}{7} - \frac{1}{8}} \right) - \left( {\frac{1}{9} - \frac{1}{{10}}} \right) - ... - \left( {\frac{1}{{2021}} - \frac{1}{{2022}}} \right) - \frac{1}{{2023}}\)
Nhận thấy \(\frac{{23}}{{60}} < \frac{{24}}{{60}}\).
Suy ra \(\frac{{23}}{{60}} - \left( {\frac{1}{7} - \frac{1}{8}} \right) - \left( {\frac{1}{9} - \frac{1}{{10}}} \right) - ... - \left( {\frac{1}{{2021}} - \frac{1}{{2022}}} \right) - \frac{1}{{2023}} < \frac{{24}}{{60}}\).
Do đó, \(M < \frac{{24}}{{60}}\) hay \(M < \frac{2}{5}\) (2)
Từ (1) và (2) ta có \(\frac{1}{5} < M < \frac{2}{5}\) (đpcm)
Lời giải
a) Ta có hình vẽ:
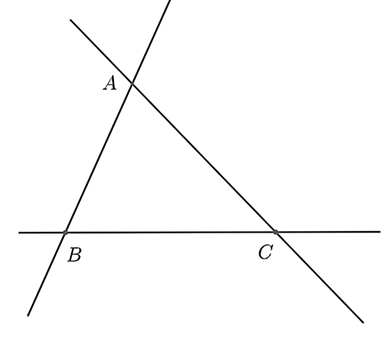
• Các đường thẳng kẻ được là \(AB,AC,BC.\)
• Giao điểm của từng cặp đường thẳng như sau:
- Hai đường thẳng \(AB,AC\) cắt nhau tại \(A\).
- Hai đường thẳng \(AB,BC\) cắt nhau tại \(B.\)
- Hai đường thẳng \(AC,BC\) cắt nhau tại \(C.\)
b)
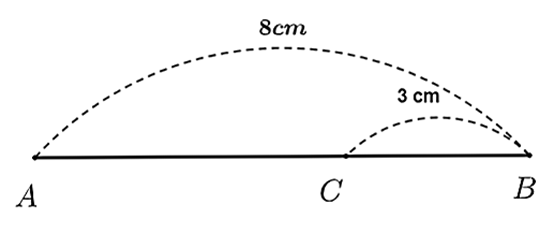
Vì điểm \(C\) nằm giữa hai điểm \(A\) và \(B\) nên ta có \(AC + BC = AB\),
do đó \(AC = AB - CB = 8 - 3 = 5{\rm{ }}\left( {{\rm{cm}}} \right)\).
Vì \(5{\rm{ cm}} > 3{\rm{ cm}}\) nên \(AC > BC.\)
Vậy \(AC > BC.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Lớp 6A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
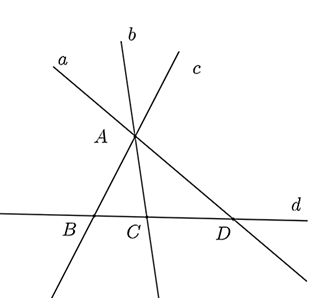 a) Điểm \(A\) thuộc các đường thẳng \(a,b,c\).
a) Điểm \(A\) thuộc các đường thẳng \(a,b,c\).