(3,0 điểm)

1. Tập hợp \(V\) được biểu diễn bằng biểu đồ Ven như trong hình vẽ dưới đây. Hãy mô tả tập hợp \(V\) bằng cách nêu dấu hiệu đặc trưng cho các phần tử của tập hợp.

2. Trong một cuộc thi “Hành trình văn hóa”, mỗi thí sinh tham dự cuộc thi được tặng trước 500 điểm. Sau đó mỗi câu trả lời đúng người đó được 500 điểm, mỗi câu trả lời sai người đó được \[ - 200\] điểm. Sau 8 câu hỏi, anh An trả lời đúng 5 câu, sai 3 câu; chị Lan trả lời đúng 3 câu, sai 5 câu; chị Trang trả lời đúng 6 câu, sai 2 câu. Tính số điểm mỗi người sau cuộc thi để tìm xem ai là người cao điểm nhất.

3. Khối 6 của một trường THCS có 60 học sinh nam và 48 học sinh nữ. Các thầy, cô muốn chia học sinh khối 6 thành các nhóm để lao động trồng cây nhân dịp Tết Nguyên đán sao cho học sinh nam trong mỗi nhóm bằng nhau và số học sinh nữ trong mỗi nhóm cũng bằng nhau. Hỏi phải chia thành bao nhiêu nhóm để số học sinh trong mỗi nhóm là ít nhất? Khi đó mỗi nhóm có bao nhiêu học sinh nam và bao nhiêu học sinh nữ?

Hướng dẫn giải

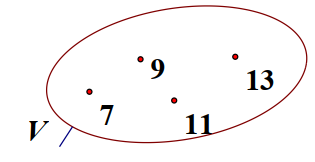
1. Mô tả tập hợp \(V\) bằng cách nêu dấu hiệu đặc trưng cho các phần tử của tập hợp:

\(V = \{ x|x\) là số tự nhiên lẻ, \(7 \le x \le 13\} \).

2. Số điểm của anh An là: \(5 \cdot 500 + 3 \cdot \left( { - 200} \right) = 1\,\,900\) (điểm)

Số điểm của chị Lan là: \(3 \cdot 500 + 5 \cdot \left( { - 200} \right) = 500\) (điểm)

Số điểm của chị Trang là: \(6 \cdot 500 + 2 \cdot \left( { - 200} \right) = 2\,\,600\) (điểm)

Vì \(2\,\,600 > 1\,\,900 > 500\) nên điểm của chị Trang cao điểm nhất.

Vậy trong 3 người thì chị Trang là người cao điểm nhất.

3. Số học sinh trong mỗi nhóm càng nhỏ thì số nhóm cần chia càng lớn.

Gọi số nhóm lớn nhất cần chia sao cho số học sinh trong mỗi nhóm ít nhất là \(x\) \(\left( {x \in \mathbb{N}} \right)\).

Để chia 60 học sinh nam và 48 học sinh nữ vào các nhóm sao cho số học sinh nam trong mỗi nhóm bằng nhau và số học sinh nữ trong mỗi nhóm bằng nhau thì \(60\,\, \vdots \,\,x,\,\,48\,\, \vdots \,\,x\)

Mà số nhóm cần chia là lớn nhất nên \(x = \)ƯCLN\(\left( {60,48} \right)\).

Ta có: \(60 = {2^2}.3.5;\,\,\,\,\,\,\,\,48 = {2^4}.3\).

Suy ra \(x = \)ƯCLN\(\left( {60,48} \right) = {2^2}.3 = 12\).

Vậy số nhóm cần chia là \(12\) nhóm.

Khi đó số học sinh nam trong mỗi nhóm là: \(60:12 = 5\) (học sinh);

Số học sinh nữ trong mỗi nhóm là: \(48:12 = 4\) (học sinh).