1) Điểm \(A\) nằm trên tia \(Ox\) sao cho \(OA = 4{\rm{\;cm}}.\) Trên tia đối của tia \(Ox\) lấy điểm \(B\) và \(M\) sao cho \(OB = 8{\rm{\;cm}}\) và \(OM = OA.\)
a) Điểm \(O\) có phải là trung điểm của đoạn thẳng \(AM\) không? Tại sao?
b) Tính độ dài đoạn thẳng \(BM\) và \(AB.\)
c) Gọi \(C\) là trung điểm của đoạn thẳng \(AB.\) Chứng minh \(C\) là trung điểm của đoạn thẳng \(OM.\)
2) Ta có thể xem kim phút và kim giờ của đồng hồ là hai tia chung gốc (gốc trùng với trục quay của hai kim). Tại mỗi thời điểm hai kim tạo thành một góc.
a) Khi kim giờ và kim phút thay nhau chỉ số 12 và số 6 thì tạo thành một góc có số đo là bao nhiêu độ?
b) Góc tạo bởi kim phút và kim giờ lúc 2 giờ có số đo là bao nhiêu độ?
1) Điểm \(A\) nằm trên tia \(Ox\) sao cho \(OA = 4{\rm{\;cm}}.\) Trên tia đối của tia \(Ox\) lấy điểm \(B\) và \(M\) sao cho \(OB = 8{\rm{\;cm}}\) và \(OM = OA.\)
a) Điểm \(O\) có phải là trung điểm của đoạn thẳng \(AM\) không? Tại sao?
b) Tính độ dài đoạn thẳng \(BM\) và \(AB.\)
c) Gọi \(C\) là trung điểm của đoạn thẳng \(AB.\) Chứng minh \(C\) là trung điểm của đoạn thẳng \(OM.\)
2) Ta có thể xem kim phút và kim giờ của đồng hồ là hai tia chung gốc (gốc trùng với trục quay của hai kim). Tại mỗi thời điểm hai kim tạo thành một góc.
a) Khi kim giờ và kim phút thay nhau chỉ số 12 và số 6 thì tạo thành một góc có số đo là bao nhiêu độ?
b) Góc tạo bởi kim phút và kim giờ lúc 2 giờ có số đo là bao nhiêu độ?
Quảng cáo
Trả lời:
1)

a) Vì điểm \(A\) thuộc tia \[Ox\] và tia \(M\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A,\,\,M.\)
Lại có \(OA = OM\) nên điểm \(O\) là trung điểm của đoạn thẳng \(AM.\)
b) ⦁ Ta có \(OM = OA = 4{\rm{\;cm}}\) và \(OB = 8{\rm{\;cm}}\) nên \(OM < OB\)
Mà hai điểm \(B\) và \(M\) nằm trên tia đối của tia \(Ox\) nên điểm \(M\) nằm giữa hai điểm \(O\) và \(B\)
Do đó \(OB = BM + OM\)
Suy ra \(BM = OB - OM = 8 - 4 = 4{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(A\) thuộc tia \[Ox\] và tia \(B\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A\) và \(B\)
Do đó \(AB = BO + OA = 8 + 4 = 12{\rm{\;(cm)}}{\rm{.}}\)
c) Vì điểm \(C\) là trung điểm của đoạn thẳng \(AB\) nên \(BC = AC = \frac{{AB}}{2} = \frac{{12}}{2} = 6{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(A\) thuộc tia \[Ox\] và tia \(C\) thuộc tia đối của tia \(Ox\) nên điểm \(O\) nằm giữa hai điểm \(A\) và \(C\)
Do đó \(AC = CO + OA\)
Suy ra \(CO = AC - OA = 6 - 4 = 2{\rm{\;(cm)}}{\rm{.}}\)
⦁ Ta có điểm \(M\) nằm giữa \(C\) và \(B\) nên \(BC = BM + CM\)
Suy ra \(CM = BC - BM = 6 - 4 = 2{\rm{\;(cm)}}{\rm{.}}\)
⦁ Vì điểm \(C\) nằm giữa hai điểm \(M,\,\,O\) và \(MC = CO = 2{\rm{\;cm}}\) nên điểm \(C\) là trung điểm của đoạn thẳng \(OM.\)
2) a) Khi kim giờ và kim phút thay nhau chỉ số 12 và số 6 thì tạo thành một góc có số đo bằng \(180^\circ .\)
b) Từ số 12 đến số 6 có 6 khoảng, như vậy, cứ hai kim lần lượt chỉ hai số cạnh nhau trên đồng hồ thì có số đo bằng \(\frac{{180^\circ }}{6} = 30^\circ .\)
Vậy góc tạo bởi kim phút và kim giờ lúc 2 giờ có số đo là \(2 \cdot 30^\circ = 60^\circ .\)

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Cách 1. Tỉ số vận tốc lúc lên dốc và vận tốc lúc xuống dốc là \(\frac{{10}}{{15}} = \frac{2}{3}\). Như vậy, vận tốc 10 km/h bằng \(\frac{2}{3}\) vận tốc 15 km/h.
Giả sử trong 2 giờ lúc đi, người đó đều đi với vận tốc 10 km/h thì đi được quãng đường là: \(AC + \frac{2}{3}CB,\) dài là: \(10 \cdot 2 = 20\) (km).
Giả sử trong 1 giờ 45 phút \[( = 1\frac{3}{4}\] giờ) lúc về, người đó đều đi với vận tốc 10 km/h thì đi được quãng đường \(BC + \frac{2}{3}CA,\) dài là: \(10 \cdot 1\frac{3}{4} = 17,5\) (km).
Do đó quãng đường \(20 + 17,5 = 37,5\) (km) tương ứng với
\(AC + \frac{2}{3}CB + BC + \frac{2}{3}AC = \frac{5}{3}\left( {AC + CB} \right) = \frac{5}{3}AB\)
Vậy quãng đường \(AB\) dài là: \(37,5:\frac{5}{3} = 22,5\) (km).
Cách 2. Trên mỗi km của quãng đường \[AB\] đều có một lần người đi xe đạp đi với vận tốc 10 km/h, một lần đi với vận tốc 15 km/h.
1 km đi với vận tốc 10 km/h hết \(\frac{1}{{10}}\) giờ, 1 km đi với vận tốc 15 km/h hết \(\frac{1}{{15}}\) giờ, do đó 1 km cả đi lẫn về hết: \(\frac{1}{{10}} + \frac{1}{{15}} = \frac{1}{6}\) (giờ).
Thời gian cả đi lẫn về : \(2 + 1\frac{3}{4} = 3\frac{3}{4}\) (giờ).
Quãng đường \(AB\) là: \(3\frac{3}{4}:\frac{1}{6} = 22,5\) (km).
Câu 2
1) Biểu đồ cột kép dưới đây biểu diễn số học sinh giỏi hai môn Toán và Ngữ văn của các lớp khối 6.
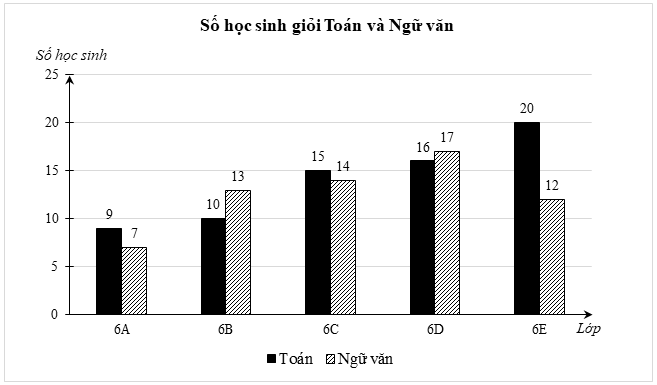
a) Số học sinh giỏi Toán của lớp nào nhiều nhất? Số học sinh giỏi Ngữ văn của lớp nào ít nhất?
b) Số học sinh giỏi Toán của lớp 6C chiếm bao nhiêu phần trăm trong tổng số học sinh giỏi môn Toán của cả 5 lớp (kết quả làm tròn đến hàng phần trăm)?
c) Bạn An nói rằng lớp 6D có 34 học sinh. Theo em, bạn An nói đúng không? Vì sao?
2) Minh gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:
Số chấm xuất hiện
1
2
3
4
5
6
Số lần
15
20
18
22
10
15
Tính xác suất thực nghiệm của sự kiện số chấm xuất hiện là số không vượt quá 4.
1) Biểu đồ cột kép dưới đây biểu diễn số học sinh giỏi hai môn Toán và Ngữ văn của các lớp khối 6.

a) Số học sinh giỏi Toán của lớp nào nhiều nhất? Số học sinh giỏi Ngữ văn của lớp nào ít nhất?
b) Số học sinh giỏi Toán của lớp 6C chiếm bao nhiêu phần trăm trong tổng số học sinh giỏi môn Toán của cả 5 lớp (kết quả làm tròn đến hàng phần trăm)?
c) Bạn An nói rằng lớp 6D có 34 học sinh. Theo em, bạn An nói đúng không? Vì sao?
2) Minh gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:
|
Số chấm xuất hiện |
1 |
2 |
3 |
4 |
5 |
6 |
|
Số lần |
15 |
20 |
18 |
22 |
10 |
15 |
Tính xác suất thực nghiệm của sự kiện số chấm xuất hiện là số không vượt quá 4.
Lời giải
1) a) Số học sinh giỏi Toán của lớp 6E là nhiều nhất (20 bạn).
Số học sinh giỏi Ngữ văn của lớp 6A là ít nhất (7 bạn).
b) Số học sinh giỏi Toán của lớp 6C chiếm số phần trăm trong tổng số học sinh giỏi môn Toán của cả 5 lớp là: \(\frac{{15}}{{9 + 10 + 15 + 16 + 20}} \cdot 100\% \approx 21,43\% .\)
c) Bạn An nói lớp 6D có sĩ số là 34 học sinh có thể chưa đúng vì trong lớp có thể có học sinh không giỏi môn Toán, hoặc học sinh không giỏi môn Ngữ văn, hoặc học sinh giỏi cả hai môn.
2) Số chấm xuất hiện là số không vượt quá 4 là: 1 chấm, 2 chấm, 3 chấm, 4 chấm.
Số lần xuất hiện mặt có số chấm không vượt quá 4 là: \[15 + 20 + 18 + 22 = 75.\]
Xác suất thực nghiệm của sự kiện số chấm xuất hiện là số không vượt quá 4 là: \(\frac{{75}}{{100}} = \frac{3}{4}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.