Một hộp có 7 quả bóng có kích thước giống nhau và được đánh số lần lượt là \(1;2;3;\)\(4;5;6;7\). Rút ngẫu nhiên một quả bóng trong hộp.
a) Viết tập hợp \(M\) gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra.
b) Tính xác suất của biến cố \(A\): “Rút được thẻ ghi số là số chẵn”.
c) Tính xác suất của biến cố \(B\): “Rút được thẻ ghi số là số chia cho 5 dư 2”.
Một hộp có 7 quả bóng có kích thước giống nhau và được đánh số lần lượt là \(1;2;3;\)\(4;5;6;7\). Rút ngẫu nhiên một quả bóng trong hộp.
a) Viết tập hợp \(M\) gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra.
b) Tính xác suất của biến cố \(A\): “Rút được thẻ ghi số là số chẵn”.
c) Tính xác suất của biến cố \(B\): “Rút được thẻ ghi số là số chia cho 5 dư 2”.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra là:
\(M = \left\{ {1;2;3;4;5;6;7} \right\}\).
Do đó, có \(7\) kết quả có thể xảy ra.
b) Kết quả thuận lợi của biến cố: “Rút được thẻ ghi số là số chẵn” là: \(2;4;6\).
Xác suất của biến cố \(A\) là \(\frac{3}{7}\).
c) Kết quả thuận lợi của biến cố: “Rút được thẻ ghi số là số chia 5 dư 2” là \(2;7\).
Xác suất của biến cố \(B\) là \(\frac{2}{7}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có, hai số cuối của số điện thoại là hai chữ số khác nhau được lập từ bộ số \(\left\{ {0;1;2;3;4;5;6;7;8;9} \right\}.\)
Vậy thì số thứ nhất trong hai số cuối đó có 10 cách chọn, số còn lại có 9 cách chọn do hai số đó là hai số khác nhau.
Vì vậy, số kết quả có thể xảy ra là: \(9.10 = 90\) (kết quả).
Vì chỉ có 1 số điện thoại cần gọi đúng nên xác suất của biến cố “Người đó bấm thử một lần được đúng số điện thoại cần gọi” là: \(\frac{1}{{90}}.\)
Lời giải
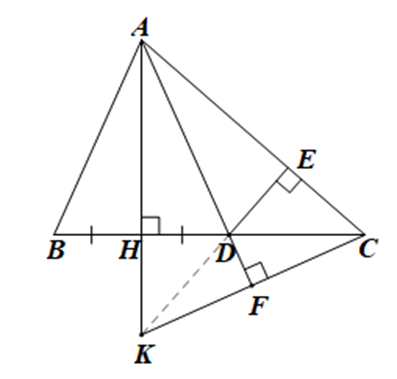
a) Xét \(\Delta ABC\) có \(AB < AC\) nên \(\widehat C < \widehat B\).
Mà \(\widehat C = 90^\circ - \widehat {HAC}\) và \(\widehat B = 90^\circ - \widehat {BAH}\).
Do đó \[90^\circ - \widehat {HAC} < 90^\circ - \widehat {BAH}\] hay \(\widehat {HAC} > \widehat {BAH}\).
b) Xét \(\Delta ABH\) và \(\Delta ADH\) có:
\(\widehat {AHB} = \widehat {AHD} = 90^\circ \);
\(AH\) là cạnh chung;
\(HB = HD\) (giả thiết).
Do đó \(\Delta ABH = \Delta ADH\) (hai cạnh góc vuông).
Suy ra \(AB = AD\) (hai cạnh tương ứng).
Tam giác \(ABD\) có \(AB = AD\) nên là tam giác cân tại \(A\).
c) Kéo dài \(AH\) và \(CF\) cắt nhau tại \(K\).
Xét \(\Delta AKC\) có \(CH \bot AK,AF \bot CK\), \(CH\) cắt \[AF\] tại \(D\) nên \(D\) là trực tâm của \(\Delta AKC\).
Suy ra \(KD \bot AC\)
Mà \(DE \bot AC\) nên ba điểm \(K,D,E\) thẳng hàng.
Vậy ba đường thẳng \(AH,DE,CF\) đồng quy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo