Bộ 12 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 09
20 người thi tuần này 4.6 7 K lượt thi 5 câu hỏi 45 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
6 câu Trắc nghiệm Toán 7 Bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh có đáp án (Vận dụng)
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
9 câu Trắc nghiệm Toán 7 Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc có đáp án (Thông hiểu)
5 câu Trắc nghiệm Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng có đáp án (Nhận biết)
4 câu Trắc nghiệm Toán 7 Bài 5: Tính chất tia phân giác của một góc có đáp án (Thông hiểu)
5 câu Trắc nghiệm Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
1.1.
|
a) \(\frac{x}{{ - 6}} = \frac{3}{4}\) \(4x = 3.\left( { - 6} \right)\) \(4x = - 18\) \(x = \frac{{ - 18}}{4}\) \(x = \frac{{ - 9}}{2}\). Vậy \(x = \frac{{ - 9}}{2}\). |
b) \(\frac{{2x + 1}}{6} = \frac{{3 - x}}{9}\) \(9\left( {2x + 1} \right) = 6\left( {3 - x} \right)\) \(18x + 9 = 18 - 6x\) \(18x + 6x = 18 - 9\) \(24x = 9\) \(x = \frac{3}{8}\). Vậy \(x = \frac{3}{8}\). |
1.2. Gọi \[a\], \(b\), \(c\) (quyển vở) lần lượt là số quyển vở lớp \(7A\), \(7B\), \(7C\) quyên góp được.
Theo đề, ta có tổng số quyển vở lớp \(7A\) và \(7B\) quyên góp được nhiều hơn lớp \(7C\) là 62 quyển, suy ra \(a + b - c = 62\).
Do số quyển vở mỗi lớp quyên góp được tỉ lệ thuận với số học sinh của lớp đó nên: \(\frac{a}{{32}} = \frac{b}{{35}} = \frac{c}{{36}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được: \(\frac{a}{{32}} = \frac{b}{{35}} = \frac{c}{{36}} = \frac{{a + b - c}}{{32 + 35 - 36}} = \frac{{62}}{{31}} = 2\).
Suy ra \(a = 32.2 = 64\); \(b = 35.2 = 70\); \(c = 36.2 = 72\).
Vậy số quyển vở lớp \(7A\), \(7B\), \(7C\) quyên góp được lần lượt là 64 quyển vở; 70 quyển vở và 72 quyển vở.
Lời giải
2.1. Thay \(x = - 1;y = 1;z = - 1\) vào biểu thức \(A = \frac{{x - 2y - z}}{2}\), ta được:
\(A = \frac{{ - 1 - 2.1 - \left( { - 1} \right)}}{2} = \frac{{ - 1 - 2 + 1}}{2} = - 1\).
Vậy giá trị của biểu thức \(A = - 1\).
2.2. a) \(A\left( x \right) = \frac{3}{4}{x^3} - 1 + \frac{3}{5}x + 4{x^2} + \frac{5}{4}{x^3} - \frac{8}{5}x + 4 + 7{x^2}\)
\( = \left( {\frac{3}{4} + \frac{5}{4}} \right){x^3} + \left( {4 + 7} \right){x^2} + \left( {\frac{3}{5} - \frac{8}{5}} \right)x - 1 + 4\)
\( = 2{x^3} + 11{x^2} - x + 3\).
b) Bậc của đa thức \(A\left( x \right)\) là 3.
Hệ số cao nhất của đa thức \(A\left( x \right)\) là 2.
c) \(B\left( x \right) = \left( {{x^2} + 1} \right)\left( {2x + 11} \right) - 5x - 8\)
0\( = 2{x^3} + 11{x^2} + 2x + 11 - 5x - 8\)
\( = 2{x^3} + 11{x^2} - 3x + 3\)
Ta có \(B\left( x \right) - C\left( x \right) = A\left( x \right)\).
Suy ra \(C\left( x \right) = B\left( x \right) - A\left( x \right)\)
\( = 2{x^3} + 11{x^2} - 3x + 3 - \left( {2{x^3} + 11{x^2} - x + 3} \right)\)
\( = 2{x^3} + 11{x^2} - 3x + 3 - 2{x^3} - 11{x^2} + x - 3\)
\( = - 2x\).
d) Để tìm nghiệm của đa thức \(C\left( x \right)\), ta cho \(C\left( x \right) = 0\)
Do đó \( - 2x = 0\)
Suy ra \(x = 0\).
Vậy nghiệm của đa thức \(C\left( x \right)\) là \(x = 0\).
Lời giải
a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra là:
\(M = \left\{ {1;2;3;4;5;6;7} \right\}\).
Do đó, có \(7\) kết quả có thể xảy ra.
b) Kết quả thuận lợi của biến cố: “Rút được thẻ ghi số là số chẵn” là: \(2;4;6\).
Xác suất của biến cố \(A\) là \(\frac{3}{7}\).
c) Kết quả thuận lợi của biến cố: “Rút được thẻ ghi số là số chia 5 dư 2” là \(2;7\).
Xác suất của biến cố \(B\) là \(\frac{2}{7}\).
Lời giải
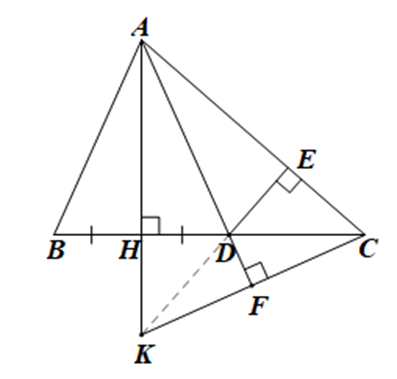
a) Xét \(\Delta ABC\) có \(AB < AC\) nên \(\widehat C < \widehat B\).
Mà \(\widehat C = 90^\circ - \widehat {HAC}\) và \(\widehat B = 90^\circ - \widehat {BAH}\).
Do đó \[90^\circ - \widehat {HAC} < 90^\circ - \widehat {BAH}\] hay \(\widehat {HAC} > \widehat {BAH}\).
b) Xét \(\Delta ABH\) và \(\Delta ADH\) có:
\(\widehat {AHB} = \widehat {AHD} = 90^\circ \);
\(AH\) là cạnh chung;
\(HB = HD\) (giả thiết).
Do đó \(\Delta ABH = \Delta ADH\) (hai cạnh góc vuông).
Suy ra \(AB = AD\) (hai cạnh tương ứng).
Tam giác \(ABD\) có \(AB = AD\) nên là tam giác cân tại \(A\).
c) Kéo dài \(AH\) và \(CF\) cắt nhau tại \(K\).
Xét \(\Delta AKC\) có \(CH \bot AK,AF \bot CK\), \(CH\) cắt \[AF\] tại \(D\) nên \(D\) là trực tâm của \(\Delta AKC\).
Suy ra \(KD \bot AC\)
Mà \(DE \bot AC\) nên ba điểm \(K,D,E\) thẳng hàng.
Vậy ba đường thẳng \(AH,DE,CF\) đồng quy.
Lời giải
Ta có, hai số cuối của số điện thoại là hai chữ số khác nhau được lập từ bộ số \(\left\{ {0;1;2;3;4;5;6;7;8;9} \right\}.\)
Vậy thì số thứ nhất trong hai số cuối đó có 10 cách chọn, số còn lại có 9 cách chọn do hai số đó là hai số khác nhau.
Vì vậy, số kết quả có thể xảy ra là: \(9.10 = 90\) (kết quả).
Vì chỉ có 1 số điện thoại cần gọi đúng nên xác suất của biến cố “Người đó bấm thử một lần được đúng số điện thoại cần gọi” là: \(\frac{1}{{90}}.\)