(4,0 điểm)

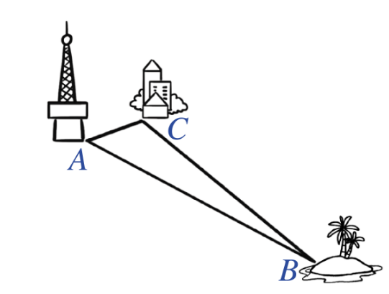
4.1. Người ta đặt một trạm phát sóng \(4G\) tại vị trí \(A\). Có một đảo nhỏ (tại vị trí \(B\)) chưa biết khoảng cách đến vị trí \(A\) nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí \(C\)) là \(75{\rm{ km}}\) và khách sạn đó cách vị trí \(A\) là \(20{\rm{ km}}\). Biết rằng sóng \(4G\) của trạm phát sóng có thể phủ đến bán kính \(100{\rm{ km}}\). Hỏi sóng \(4G\) của trạm phát sóng tại vị trí \(A\) có thể phủ đến đảo được hay không? Vì sao?

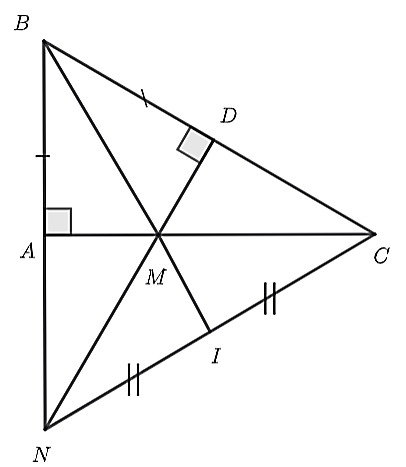
4.2.Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\). Trên cạnh \(BC\) lấy điểm \(D\) sao cho \(BD = BA\). Đường thẳng vuông góc với \(BC\) tại \(D\) cắt cạnh \(AC\) tại \(M\), cắt tia \(BA\) tại \(N.\)

a) Chứng minh \(\Delta ABM = \Delta DBM.\)

b) Chứng minh \(\Delta MNC\) cân.

c) Gọi \(I\) là trung điểm của \(CN\). Chứng minh ba điểm \(B,M,I\) thẳng hàng.

Hướng dẫn giải

4.1.Theo đề và từ hình minh họa, ta có: \(BC = 75{\rm{ km, }}AC = 20{\rm{ km}}\).

Khoảng cách từ trạm phát sóng đến hòn đảo chính là độ dài đoạn \(AB\)

Do đó, áp dụng bất đẳng thức về cạnh trong tam giác \(ABC,\) ta có:

\(BC + AC > AB\) hay \(75 + 20 > AB\) nên \(AB < 95{\rm{ km}}\).

Do đó, sóng \(4G\) của trạm phát sóng tại vị trí \(A\) có thể đến đảo.

4.2. a) Xét tam giác \(\Delta ABM\) và \(\Delta DBM\), có:

\(AB = BD\) (gt)

\(BM\) chung (gt)

\(\widehat {BAM} = \widehat {MDB} = 90^\circ \) (gt)

Do đó, \(\Delta ABM = \Delta DBM\) (ch – cgv)

b) Do \(\Delta ABM = \Delta DBM\) (cmt) nên \(AM = MD\) (hai cạnh tương ứng)

Xét \(\Delta AMN\) và \(\Delta DMC\), ta có:

\(\widehat {MAN} = \widehat {MDC} = 90^\circ \) (gt)

\(AM = MD\) (cmt)

\(\widehat {AMN} = \widehat {DMC}\) (đối đỉnh)

Suy ra \(\Delta AMN = \Delta DMC\) (cgv – gn)

Do đó, \(MN = MC\) (hai cạnh tương ứng)

Suy ra \(\Delta MNC\) cân tại \(M.\)

c) Do \(\Delta MNC\) cân tại \(M\) và \(I\) là trung điểm của \(NC\) nên \(MI\) cũng là đường cao của \(\Delta MNC\)

Suy ra \(MI \bot NC\).

Xét \(\Delta AMN\) và \(\Delta DMC,\) có:

\(\widehat {AMN} = \widehat {DMC}\) (đối đỉnh)

\(AM = MD\) (cmt)

\(MN = MC\) (cmt)

Suy ra \(\Delta AMN = \Delta DMC\) (c.g.c)

Do đó, \(AN = DC\) (hai cạnh tương ứng)

Ta có: \(AB + AN = BN;{\rm{ }}BD + DC = BC\).

Mà \(AN = DC,AB = BD\). Suy ra \(BN = BC\).

Do đó, \(\Delta BNC\) cân tại \(B\).

Suy ra \(BI \bot NC\) tại \(I\).

Mà \(MI \bot NC\) tại \(I\).

Do đó, \(B,M,I\) thẳng hàng.