Câu hỏi:
30/06/2025 24(0,5 điểm) Trong một hộp kín có chứa \(10\) bông hoa hồng đỏ, \(20\) hoa hồng vàng và \(n\) bông hoa hồng xanh. Lấy ngẫu nhiên một bông hoa trong hộp kín. Biết xác suất để lấy được bông hoa hồng xanh là \(\frac{4}{{10}}\). Tính số hoa hồng xanh có trong hộp.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Tổng số bông hoa trong hộp kín là \(10 + 20 + n = n + 30\) (bông)
Xác suất để lấy được một bông hoa hồng xanh là \(\frac{n}{{n + 30}}\).
Mà xác suất để lấy được một bông hoa hồng xanh là \(\frac{4}{{10}}\).
Do đó, ta có: \(\frac{n}{{n + 30}} = \frac{4}{{10}}\) hay \(10n = 4n + 120\), do đó \(6n = 120\) nên \(n = 20\).
Vậy trong hộp có 20 bông hoa hồng xanh.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
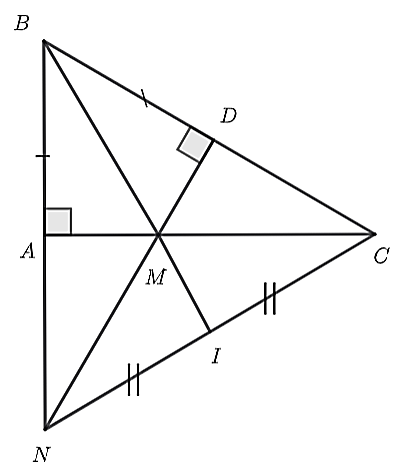
a) Xét tam giác
\(\Delta ABM\) và \(\Delta DBM\), có:
\(AB = BD\) (gt)
\(BM\) chung (gt)
\(\widehat {BAM} = \widehat {MDB} = 90^\circ \) (gt)
Do đó, \(\Delta ABM = \Delta DBM\) (ch – cgv)
b) Do \(\Delta ABM = \Delta DBM\) (cmt) nên \(AM = MD\) (hai cạnh tương ứng)
Xét \(\Delta AMN\) và \(\Delta DMC\), ta có:
\(\widehat {MAN} = \widehat {MDC} = 90^\circ \) (gt)
\(AM = MD\) (cmt)
\(\widehat {AMN} = \widehat {DMC}\) (đối đỉnh)
Suy ra \(\Delta AMN = \Delta DMC\) (cgv – gn)
Do đó, \(MN = MC\) (hai cạnh tương ứng)
Suy ra \(\Delta MNC\) cân tại \(M.\)
c) Do \(\Delta MNC\) cân tại \(M\) và \(I\) là trung điểm của \(NC\) nên \(MI\) cũng là đường cao của \(\Delta MNC\).
Suy ra \(MI \bot NC\).
Xét \(\Delta AMN\) và \(\Delta DMC,\) có:
\(\widehat {AMN} = \widehat {DMC}\) (đối đỉnh)
\(AM = MD\) (cmt)
\(MN = MC\) (cmt)
Suy ra \(\Delta AMN = \Delta DMC\) (c.g.c)
Do đó, \(AN = DC\) (hai cạnh tương ứng)
Ta có: \(AB + AN = BN;{\rm{ }}BD + DC = BC\).
Mà \(AN = DC,AB = BD\). Suy ra \(BN = BC\).
Do đó, \(\Delta BNC\) cân tại \(B\).
Suy ra \(BI \bot NC\) tại \(I\).
Mà \(MI \bot NC\) tại \(I\).
Do đó, \(B,M,I\) thẳng hàng.
Lời giải
Hướng dẫn giải
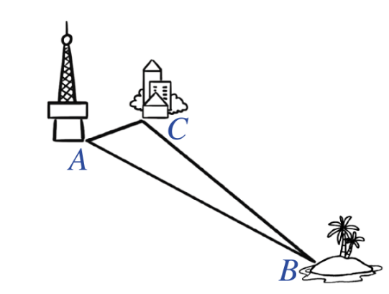
Theo đề và từ hình minh họa, ta có: \(BC = 75{\rm{ km, }}AC = 20{\rm{ km}}\).
Khoảng cách từ trạm phát sóng đến hòn đảo chính là độ dài đoạn \(AB\)
Do đó, áp dụng bất đẳng thức về cạnh trong tam giác \(ABC,\) ta có:
\(BC + AC > AB\) hay \(75 + 20 > AB\) nên \(AB < 95{\rm{ km}}\).
Do đó, sóng \(4G\) của trạm phát sóng tại vị trí \(A\) có thể đến đảo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo