1. Xét các phương trình dưới đây:

\({\left( {x - 5} \right)^2} - 11 = 0;\)                \( - \frac{3}{5}{x^3} - \frac{7}{2}x = 0;\)     \(3{x^2} - 2\sqrt 3 x + 1 = 0;\)                     \({x^2} - 2y + 5 = 0.\)

     a) Trong các phương trình trên, chỉ ra phương trình bậc hai một ẩn và các hệ số \(a,b,c\) của phương trình đó.

     b) Giải phương trình tìm được ở phần a).

2. Giải bài toán sau bằng cách lập phương trình:

Một mảnh vườn hình chữ nhật \(ABCD\) có chu vi và diện tích lần lượt là \(70{\rm{\;m}}\) và \(250{\rm{\;}}{{\rm{m}}^2}.\) Người ta chia mảnh vườn đó thành ba khu vực: khu tiểu cảnh \(ADE,\) khu trồng hoa \(BEDF,\) khu thư giãn \(BCF\) với \(BE = DF = 6{\rm{\;m}}\) như mô tả ở hình bên.

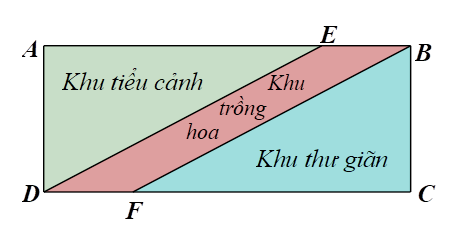
Người chủ vườn đã thuê người trồng hoa ở khu trồng hoa với chi phí là 50 000 đồng/m2. Tính số tiền chủ vườn phải trả cho người trồng hoa để trồng hết khu vườn hoa đó.

     a) Thay \(x = 1,y =  - 2\) vào \(\left( P \right)\), ta được: \(a =  - 2\).

     Vậy hàm số đi qua điểm \(A\left( {1; - 2} \right)\) là \(y =  - 2{x^2}\).

     b) Ta có bảng giá trị của hàm số \(y =  - 2{x^2}\) như sau:                       

     Do đó, đồ thị hàm số đi qua các điểm có tọa độ là \(\left( { - 2; - 8} \right);\left( { - 1; - 2} \right);\left( {0;0} \right);\)                                   \(\left( {1; - 2} \right);\left( {2; - 8} \right)\).

     Ta có đồ thị hàm số như sau:

     c) Thay \(x = \frac{2}{3}\) vào \(\left( P \right)\), ta có: \(y =  - 2.{\left( {\frac{2}{3}} \right)^2}\) hay \(y = \frac{{ - 8}}{9}\).

     Do đó, điểm thuộc \(\left( P \right)\) có hoành độ là \(\frac{2}{3}\) đó là \(\left( {\frac{2}{3};\frac{{ - 8}}{9}} \right)\).

     a) Với \(m = 2,\) ta có: \(\left( {2.2 - 3} \right){x^2} - 2\left( {2 - 2} \right)x - 1 = 0\) hay \({x^2} - 1 = 0\) nên \({x^2} = 1\).

     Suy ra \(x = 1\) hoặc \(x =  - 1\).

     Vậy với \(m = 2,\) phương trình có nghiệm là \(\left\{ { - 1;1} \right\}\).

     b) Xét phương trình \(\left( {2m - 3} \right){x^2} - 2\left( {m - 2} \right)x - 1 = 0\({\left( {m - 1} \right)^2} > 0\)\), ta có:

     • Với \(2m - 3 = 0\) thì \(m = \frac{3}{2}\) thì ta được: \(x - 1 = 0\), suy ra \(x = 1\). (1)

     • Với \(2m - 3 \ne 0\) thì \(m \ne \frac{3}{2}\) ta được phương trình bậc hai \(\left( {2m - 3} \right){x^2} - 2\left( {m - 2} \right)x - 1 = 0\)

     Có \(\Delta ' = {\left[ { - \left( {m - 2} \right)} \right]^2} + \left( {2m - 3} \right) = {m^2} - 2m + 1 = {\left( {m - 1} \right)^2} \ge 0\), với mọi \(m \in \mathbb{R}\). (2)

     Từ (1) và (2), suy ra phương trình luôn có nghiệm với mọi \(m \in \mathbb{R}\).

c) Để phương trình có hai nghiệm phân biệt thì \(\Delta ' > 0\) và \(2m - 3 \ne 0\), suy ra  và \(m \ne \frac{3}{2}\), do đó \(m \ne 1\) và \(m \ne \frac{3}{2}\).

     Theo hệ thức Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{2\left( {m - 2} \right)}}{{2m - 3}}\\{x_1}{x_2} = \frac{{ - 1}}{{\left( {2m - 3} \right)}}\end{array} \right.\).

     Mà theo đề, ta có: \(2{x_1} + 3{x_2} = 5\) suy ra \({x_1} = \frac{{5 - 3{x_2}}}{2}\).

     Thay \({x_1} = \frac{{5 - 3{x_2}}}{2}\) vào \({x_1} + {x_2} = \frac{{2\left( {m - 2} \right)}}{{2m - 3}}\), ta được: \(\frac{{5 - 3{x_2}}}{2} + {x_2} = \frac{{2\left( {m - 2} \right)}}{{2m - 3}}\).

     Suy ra \(5 - {x_2} = \frac{{4\left( {m - 2} \right)}}{{2m - 3}}\) nên \({x_2} = 5 - \frac{{4\left( {m - 2} \right)}}{{2m - 3}} = \frac{{6m - 7}}{{2m - 3}}\).

     Do đó, \({x_1} = \frac{{5 - 3{x_2}}}{2} = \frac{5}{2} - \frac{3}{2}{x_2} = \frac{5}{2} - \frac{3}{2}.\frac{{6m - 7}}{{2m - 3}} = \frac{{ - 8m + 6}}{{2\left( {2m - 3} \right)}} = \frac{{ - 4m + 3}}{{2m - 3}}\).

Mà \({x_1}{x_2} = \frac{{ - 1}}{{\left( {2m - 3} \right)}}\) nên \(\frac{{6m - 7}}{{\left( {2m - 3} \right)}}.\frac{{\left( { - 4m + 3} \right)}}{{\left( {2m - 3} \right)}} = \frac{{ - 1}}{{2m - 3}}\).

Suy ra \(\left( {6m - 7} \right).\left( { - 4m + 3} \right) =  - \left( {2m - 3} \right)\)

Do đó, \(24{m^2} - 46m + 21 = 2m - 3\) hay \(24{m^2} - 48m + 24 = 0\)

Suy ra \({m^2} - 2m + 1 = 0\) hay \({\left( {m - 1} \right)^2} = 0\).

Suy ra \(m = 1\) (loại).

Vậy không có giá trị của \(m\) thỏa mãn yêu cầu bài toán.