Cho parabol \(\left( P \right):y = m{x^2}\).
a) Tìm \(m\) để \(\left( P \right)\) đi qua điểm \(A\left( {2;1} \right)\).
b) Vẽ \(\left( P \right)\) khi \(m = - \frac{1}{2}\).
c) Với \(m = - \frac{1}{2}\), tìm điểm có tung độ bằng \( - 8.\)
d) Với \(m = - \frac{1}{2}\), hãy tìm điểm thuộc parabol mà có tổng hoành độ và tung độ bằng \(0.\)
Cho parabol \(\left( P \right):y = m{x^2}\).
a) Tìm \(m\) để \(\left( P \right)\) đi qua điểm \(A\left( {2;1} \right)\).
b) Vẽ \(\left( P \right)\) khi \(m = - \frac{1}{2}\).
c) Với \(m = - \frac{1}{2}\), tìm điểm có tung độ bằng \( - 8.\)
d) Với \(m = - \frac{1}{2}\), hãy tìm điểm thuộc parabol mà có tổng hoành độ và tung độ bằng \(0.\)
Quảng cáo
Trả lời:
a) Thay \(x = 2,y = 1\)vào hàm số \(\left( P \right):y = m{x^2}\), ta được: \(4m = 1\) nên \(m = \frac{1}{4}.\)
Vậy \(\left( P \right):y = \frac{1}{4}{x^2}\) thì đi qua điểm \(A\left( {2;1} \right)\).
b) Với \(m = - \frac{1}{2}\), ta có: \(\left( P \right):y = - \frac{1}{2}{x^2}\).
Lập bảng giá trị, ta có:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = - \frac{1}{2}{x^2}\) |
\( - 2\) |
\( - \frac{1}{2}\) |
\(0\) |
\( - \frac{1}{2}\) |
\( - 2\) |
Ta có đồ thị hàm số sau:
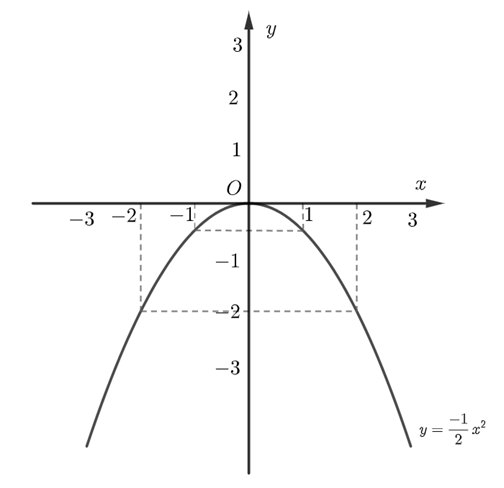
c) Có \(y = - \frac{1}{2}{x^2}\), thay \(y = - 8\) vào hàm số ta có: \( - \frac{1}{2}{x^2} = - 8\) nên \({x^2} = 16\).
Do \(x = 4\) hoặc \(x = - 4\).
Vậy với \(m = - \frac{1}{2}\), điểm có tọa độ \(\left( {4; - 8} \right);\left( { - 4; - 8} \right)\).
d) Gọi \(I\left( {{x_0}; - \frac{1}{2}x_0^2} \right)\) là điểm có tổng hoành độ và tung độ bằng \(0.\)
Ta có: \( - \frac{1}{2}x_0^2 + {x_0} = 0\) hay \({x_0}\left( { - \frac{1}{2}{x_0} + 1} \right) = 0\), suy ra \({x_0} = 0\) hoặc \({x_0} = 2\).
Với \({x_0} = 0\) thì \({y_0} = - \frac{1}{2}\).
Với \({x_0} = 2\) thì \({y_0} = - 2.\)
Vậy điểm thỏa mãn có \(\left( {0;0} \right),\left( {2; - 2} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
1. Xét \(\Delta ABC\) đều có \(AB = AC\) và \(\widehat {BAC} = 60^\circ \). Phép quay thuận chiều kim đồng hồ với tâm \(A\) biến điểm \(B\) thành điểm \(C\) tạo nên cung lớn \(BC\) có số đo là:
Vậy góc quay của phép quay đó là \(300^\circ .\) |
 |
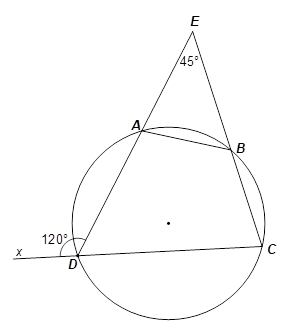
2. Ta có \(\widehat {ADx} + \widehat {ADC} = 180^\circ \) (hai góc kề bù)
Tứ giác \(ABCD\) nội tiếp đường tròn nên \(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (tổng hai góc đối nhau trong một tứ giác nội tiếp).
Suy ra \(\widehat {ABC} = \widehat {ADx} = 120^\circ .\)
Mà \(\widehat {ABC}\) là góc ngoài tại đỉnh \(B\) của tam giác \(ABE\) nên \(\widehat {ABC} = \widehat {AEB} + \widehat {BAE}\)
Suy ra \(\widehat {BAE} = \widehat {ABC} - \widehat {AEB} = 120^\circ - 45^\circ = 75^\circ .\)
Lại có \(\widehat {BAE} + \widehat {BAD} = 180^\circ \) (hai góc kề bù) và \(\widehat {BCD} + \widehat {BAD} = 180^\circ \) (tổng hai góc đối nhau trong tứ giác \(ABCD\) nội tiếp).
Suy ra \(\widehat {BCD} = \widehat {BAE} = 75^\circ .\)
Lời giải
a) Phương trình \({x^2} - 2mx - 2{m^2} - 1 = 0\) có \(\Delta ' = {\left( { - m} \right)^2} + 2{m^2} + 1 = 3{m^2} + 1 > 0\) với mọi \(m\).
Do đó, phương trình luôn có nghiệm.
b) Với \(m = 2,\) ta có: \({x^2} - 4x - 9 = 0\).
Ta có biệt thức \(\Delta ' = {\left( { - 2} \right)^2} - \left( { - 9} \right) = 13 > 0\).
Do đó, phương trình có hai nghiệm phân biệt.
Đó là \({x_1} = 2 - \sqrt {13} \) và \({x_2} = 2 + \sqrt {13} \).
Vậy tập nghiệm của phương trình là \(\left\{ {2 - \sqrt {13} ;2 + \sqrt {13} } \right\}\).
c) Xét phương trình \({x^2} - 2mx - 2{m^2} - 1 = 0\) có:
\(\Delta ' = {\left( { - m} \right)^2} - 1 \cdot \left( { - 2{m^2} - 1} \right) = {m^2} + 2{m^2} + 1 = 3{m^2} + 1.\)
Với mọi \(m \in \mathbb{R}\) ta thấy \(3{m^2} + 1 > 0\) nên \(\Delta ' > 0.\)
Do đó, phương trình đã cho có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) với mọi giá trị của \(m.\)
Theo định lí Viète, ta có: \({x_1} + {x_2} = 2m;\,\,{x_1}{x_x} = - 2{m^2} - 1.\)
Ta có: \(\frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}} = - 3\)
\(\frac{{x_1^2 + x_2^2}}{{{x_1}{x_2}}} = - 3\)
\(\frac{{x_1^2 + 2{x_1}{x_2} + x_2^2 - 2{x_1}{x_2}}}{{{x_1}{x_2}}} = - 3\)
\(\frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}}}{{{x_1}{x_2}}} = - 3\)
\(\frac{{{{\left( {2m} \right)}^2} - 2\left( { - 2{m^2} - 1} \right)}}{{ - 2{m^2} - 1}} = - 3\)
\(4{m^2} + 4{m^2} + 2 = 6{m^2} + 3\)
\(2{m^2} = 1\)
\({m^2} = \frac{1}{2}\)
\(m = \frac{{\sqrt 2 }}{2}\) (thỏa mãn) hoặc \(m = - \frac{{\sqrt 2 }}{2}\) (thỏa mãn).
Vậy \(m \in \left\{ {\frac{{\sqrt 2 }}{2};\,\, - \frac{{\sqrt 2 }}{2}} \right\}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.