Phương trình \[x - 5y = 2\] nhận cặp số nào sau đây làm nghiệm?
A. \[\left( {1\,;\,\, - 2} \right)\].
B. \[\left( {3\,;\,\, - 1} \right)\].
C. \[\left( { - 1\,;\,\, - 3} \right)\].
D. \(\left( {7\,;\,\,1} \right).\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
• Thay \[x = 1\,;{\rm{ }}y = - 2\] vào phương trình đường thẳng, ta có: \[1 - 5 \cdot \left( { - 2} \right) = 11 \ne 2.\]
Suy ra \[\left( {1\,;\,\, - 2} \right)\] không phải là nghiệm của phương trình \[x - 5y = 2\].
• Thay \[x = 3\,;{\rm{ }}y = - 1\] vào phương trình đường thẳng, ta có: \[3 - 5 \cdot \left( { - 1} \right) = 8 \ne 2.\]
Suy ra \[\left( {3\,;\,\, - 1} \right)\] không phải là nghiệm của phương trình \[x - 5y = 2\].
• Thay \[x = - 1\,;{\rm{ }}y = - 3\] vào phương trình đường thẳng, ta có: \[ - 1 - 5 \cdot \left( { - 3} \right) = 14 \ne 2.\]
Suy ra \[\left( { - 1\,;\,\, - 3} \right)\] không phải là nghiệm của phương trình \[x - 5y = 2\].
• Thay \[x = 7\,;{\rm{ }}y = 1\] vào phương trình đường thẳng, ta có: \[7 - 5 \cdot 1 = 7 - 5 = 2.\]
Suy ra \(\left( {7\,;\,\,1} \right)\) là nghiệm của phương trình \[x - 5y = 2\].
Do đó, ta chọn đáp án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
1. Xét tam giác \[ABC\] vuông tại \(A\), ta có:
\(AB = BC\,.\,\cos C\) nên
\(BC = \frac{{AB}}{{\cos C}} = \frac{6}{{\frac{3}{5}}} = 10\,\,\left( {{\rm{cm}}} \right)\).
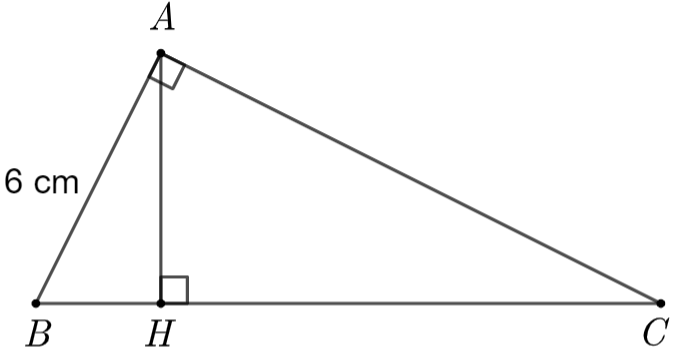
Áp dụng định lí Pythagore, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
\(A{C^2} = B{C^2} - A{B^2} = {10^2} - {6^2} = 64\), suy ra \(AC = 8\,\,{\rm{cm}}\).
Xét \(\Delta ABH\) và \(\Delta CBA\) có \(\widehat {AHB} = \widehat {BAC} = 90^\circ ;\,\,\widehat B\) chung.
Do đó .
Suy ra \(\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\) hay \(A{B^2} = BH\,.\,BC\) nên \(BH = \frac{{A{B^2}}}{{BC}} = \frac{{{6^2}}}{{10}} = 3,6\,\,\left( {{\rm{cm}}} \right)\).
Vậy \(BC = 10\,\,{\rm{cm}},\,\,AC = 8\,\,{\rm{cm}},\,\,BH = 3,6\,\,{\rm{cm}}.\)
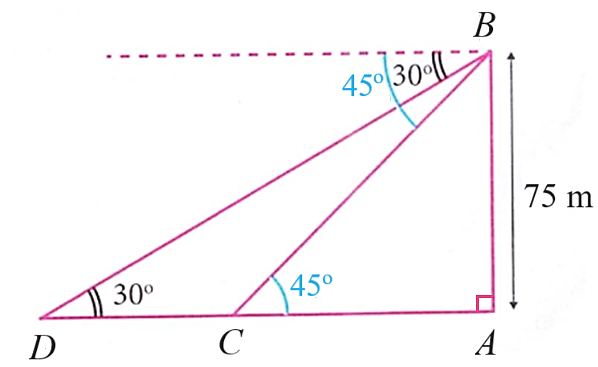
2. Quãng đường chiếc thuyền đi được giữa hai lần quan sát là \(CD.\)
Xét \(\Delta BAC\) vuông tại \(A\) có \(AC = 75\cot \widehat {BCA} = 75\cot 45^\circ = 75\,\,\left( {\rm{m}} \right)\).
Xét \(\Delta DAB\) vuông tại \(A\) có \(AD = 75\cot \widehat {BDA} = 75\cot 30^\circ = 75\sqrt 3 \,\,\left( {\rm{m}} \right)\).
Quãng đường chiếc thuyền đi được giữa hai lần quan sát là:
\(CD = AD - AC = 75\sqrt 3 - 75 \approx 55\,\,\left( {\rm{m}} \right)\).
Vậy chiếc thuyền đi được khoảng 55 mét giữa hai lần quan sát.
Lời giải
Hướng dẫn giải
Ta có: \[{x^2} + 2{y^2} + 2xy + 7x + 7y + 10 = 0.\]
\(\left( {{x^2} + 2xy + {y^2}} \right) + 7x + 7y + {y^2} + 10 = 0\)
\({\left( {x{\rm{ }} + {\rm{ }}y} \right)^2} + 7\left( {x + y} \right) + {y^2} + 10 = 0 & \left( 1 \right)\)
Đặt \[S = x + y\].
Khi đó phương trình \(\left( 1 \right)\) trở thành: \[{S^2} + 7S + {y^2} + 10 = 0\]
\({S^2} + 7S + \frac{{49}}{4} = \frac{9}{4} - {y^2}\)
\({\left( {S + \frac{7}{2}} \right)^2} = \frac{9}{4} - {y^2} \le \frac{9}{4}\).
Dấu xảy ra khi và chỉ khi \(\frac{9}{4} - {y^2} = \frac{9}{4}\) hay \(y = 0\).
Do đó \({\left( {S + \frac{7}{2}} \right)^2} \le \frac{9}{4}\) nên \(\frac{{ - 3}}{2} \le S + \frac{7}{2} \le \frac{3}{2}\) hay \[ - 5 \le S \le - 2.\]
Ta có \(P = \frac{{2x + 2y - 3}}{{x + y + 6}} = \frac{{2\left( {x + y + 6} \right) - 15}}{{x + y + 6}}\) \( = 2 - \frac{{15}}{{x + y + 6}} = 2 - \frac{{15}}{{S + 6}} & \left( 2 \right)\)
Với \[ - \,5 \le S \le - \,2\] thì \(1 \le S + 6 \le 4\)
\(\frac{{15}}{4} \le \frac{{15}}{{S + 6}} \le 15\)
\(2 - 15 \le 2 - \frac{{15}}{{S + 6}} \le 2 - \frac{{15}}{4}\)
\( - 13 \le 2 - \frac{{15}}{{S + 6}} \le - \frac{7}{4}\)
\( - 13 \le P \le - \frac{7}{4}\).
Vậy giá trị nhỏ nhất của biểu thức \[P\] là \[ - 13\] khi \(x = - 5\,;\,\,y = 0\).
Và giá trị lớn nhất của biểu thức \(P\) là \(\frac{{ - 7}}{4}\) khi \[x = - 2\,;\,\,y = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
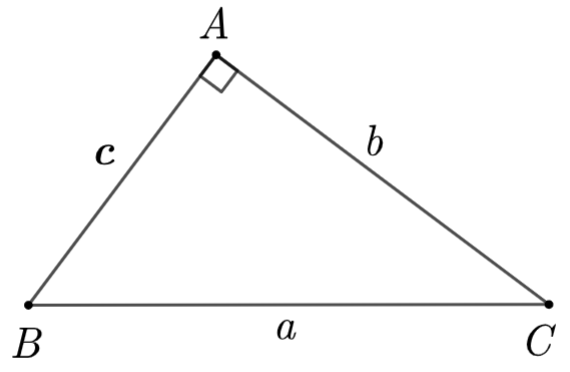
A. \[c = b \cdot \tan B\].
B. \[c = b \cdot \cot C\].
C. \[c = b \cdot \tan C\].
D. \[c = b \cdot \sin B\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
B. \[5x - 3z = 6\].
C. \(5x - 8y = 0.\)
D. \[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.