Đề thi giữa kì 1 môn Toán lớp 9 Kết nối tri thức có đáp án (Đề 6)
16 người thi tuần này 4.6 4.7 K lượt thi 17 câu hỏi 60 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
15 câu Trắc nghiệm Toán 9 Chân trời sáng tạo Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 1
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. \[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
B. \[5x - 3z = 6\].
C. \(5x - 8y = 0.\)
D. \[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Lời giải
Phương trình bậc nhất hai ẩn có dạng \[ax + by = c\] với \(a \ne 0\) hoặc \(b \ne 0\).
Xét các đáp án, ta thấy:
\[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\] hay \(x - 5 + 2y - 6 = 0\) suy ra \(x + 2y = 11\) nên đáp án A là phương trình bậc nhất hai ẩn.
\[5x - 3z = 6\] là phương trình bậc nhất hai ẩn \(x,z\) nên đáp án B là phương trình bậc nhất hai ẩn.
\(5x - 8y = 0\) là phương trình bậc nhất hai ẩn \(x,y\)
\[\left( {x - 2} \right)\left( {2y - 3} \right) = 3\] hay \[2xy - 3x - 4y + 6 = 3\] suy ra \[2xy - 3x - 4y = - 3\] nên đáp án D không là phương trình bậc nhất hai ẩn.
Chọn đáp án D.
Câu 2
A. \[\left( {1\,;\,\, - 2} \right)\].
B. \[\left( {3\,;\,\, - 1} \right)\].
C. \[\left( { - 1\,;\,\, - 3} \right)\].
D. \(\left( {7\,;\,\,1} \right).\)
Lời giải
• Thay \[x = 1\,;{\rm{ }}y = - 2\] vào phương trình đường thẳng, ta có: \[1 - 5 \cdot \left( { - 2} \right) = 11 \ne 2.\]
Suy ra \[\left( {1\,;\,\, - 2} \right)\] không phải là nghiệm của phương trình \[x - 5y = 2\].
• Thay \[x = 3\,;{\rm{ }}y = - 1\] vào phương trình đường thẳng, ta có: \[3 - 5 \cdot \left( { - 1} \right) = 8 \ne 2.\]
Suy ra \[\left( {3\,;\,\, - 1} \right)\] không phải là nghiệm của phương trình \[x - 5y = 2\].
• Thay \[x = - 1\,;{\rm{ }}y = - 3\] vào phương trình đường thẳng, ta có: \[ - 1 - 5 \cdot \left( { - 3} \right) = 14 \ne 2.\]
Suy ra \[\left( { - 1\,;\,\, - 3} \right)\] không phải là nghiệm của phương trình \[x - 5y = 2\].
• Thay \[x = 7\,;{\rm{ }}y = 1\] vào phương trình đường thẳng, ta có: \[7 - 5 \cdot 1 = 7 - 5 = 2.\]
Suy ra \(\left( {7\,;\,\,1} \right)\) là nghiệm của phương trình \[x - 5y = 2\].
Do đó, ta chọn đáp án D.
Câu 3
A. \[A\] và \[B\].
B. \[B\] và \[C\].
C. \[C\] và \[D\].
D. \[D\] và \[A\].
Lời giải
• Thay \[x = 0\,;{\rm{ }}y = 4\] vào phương trình đường thẳng, ta có:
\[4 \cdot 0--3 \cdot 4 = 0--12 = --12 \ne --1.\]
Suy ra đường thẳng \[4x--3y = --1\] không đi qua \[A\left( {0\,;\,\,4} \right)\].
Do đó, loại đáp án A và D.
• Thay \[x = 1\,;{\rm{ }}y = 5\] vào phương trình đường thẳng, ta có:
\[4 \cdot 1--3 \cdot 5 = 4--15 = --11 \ne --1.\]
Suy ra đường thẳng \[4x--3y = --1\] không đi qua \[B\left( {1\,;\,\,5} \right)\].
Do đó, loại đáp án B.
• Thay \[x = 2\,;{\rm{ }}y = 3\] vào phương trình đường thẳng, ta có:
\[4 \cdot 2--3 \cdot 3 = 8--9 = --1.\]
Suy ra đường thẳng \[4x--3y = --1\] đi qua \[C\left( {2\,;\,\,3} \right)\].
Do đó, ta chọn đáp án C.
Câu 4
A. \[\left( { - 3\,;\,\,2} \right)\].
B. \[\left( {3\,;\,\,2} \right)\].
C. \[\left( {3\,;\,\, - 2} \right)\].
D. \[\left( { - 3\,;\,\, - 2} \right).\]
Lời giải
Từ phương trình thứ nhất ta có \[y = 5 - x\]. Thế vào phương trình thứ hai, ta được
\[2x - \left( {5 - x} \right) = 4\], tức là \[3x - 5 = 4\], suy ra \[3x = 9\] hay \[x = 3\].
Từ đó \[y = 5 - 3 = 2.\]
Vậy hệ phương trình đã cho có nghiệm là \[\left( {3\,;\,\,2} \right).\]
Câu 5
A. \[x \ne - 2;{\rm{ }}x \ne 3\].
B. \[x \ne 2;{\rm{ }}x \ne --3\].
C. \[x \ne - 3;{\rm{ }}x \ne --2\].
D. \[x \ne 0;{\rm{ }}x \ne 3\].
Lời giải
Vì \[x + 2 \ne 0\] khi \[x \ne - 2\] và \[x - 3 \ne 0\] khi \[x \ne 3\] nên điều kiện xác định của phương trình \(\frac{x}{{x - 3}} = \frac{{5x}}{{\left( {x + 2} \right)\left( {x - 3} \right)}}\) là \[x \ne - 2\] và \[x \ne 3\].
Câu 6
A. \(m\) lớn hơn âm 8.
B. \(m\) không nhỏ hơn âm 8.
C. \(m\) nhỏ hơn âm 8.
D. \(m\) không lớn hơn âm 8.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[ \ge \].
B. \[ \le \].
C. \[ < \].
</>
D. \[ > \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \[3x + y > 4\].
B. \[0x - 4 \ge 0\].
C. \[5x--3 > 4\;\].
D. \[2{x^2} - 3x + 1 \le 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(\frac{3}{5}\).
B. \(\frac{4}{5}\).
C. \(\frac{5}{4}\).
D. \(\frac{5}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[\sin B--\cos C = 0.\]
B. \[\sin C + \cos {\rm{ }}B = 0.\]
C. \[\sin {\rm{ }}B + \cos {\rm{ }}C = 0.\]
D. \[\cos B + \cos C = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
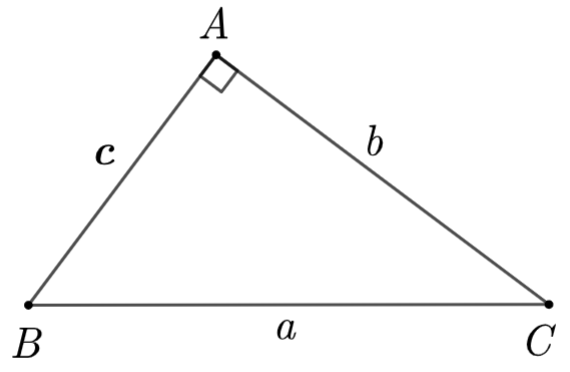
A. \[c = b \cdot \tan B\].
B. \[c = b \cdot \cot C\].
C. \[c = b \cdot \tan C\].
D. \[c = b \cdot \sin B\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. 4 cm.
B. \(8\sqrt 3 \,\,{\rm{cm}}\).
C. \(\frac{{8\sqrt 3 }}{3}\,\,{\rm{cm}}\).
D. 16 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.