Bất đẳng thức \(m \le - 8\) có thể được phát biểu là
A. \(m\) lớn hơn âm 8.
B. \(m\) không nhỏ hơn âm 8.
C. \(m\) nhỏ hơn âm 8.
D. \(m\) không lớn hơn âm 8.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
Bất đẳng thức \(m \le - 8\) có thể được phát biểu là \(m\) không lớn hơn âm 8.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
1. Xét tam giác \[ABC\] vuông tại \(A\), ta có:
\(AB = BC\,.\,\cos C\) nên
\(BC = \frac{{AB}}{{\cos C}} = \frac{6}{{\frac{3}{5}}} = 10\,\,\left( {{\rm{cm}}} \right)\).
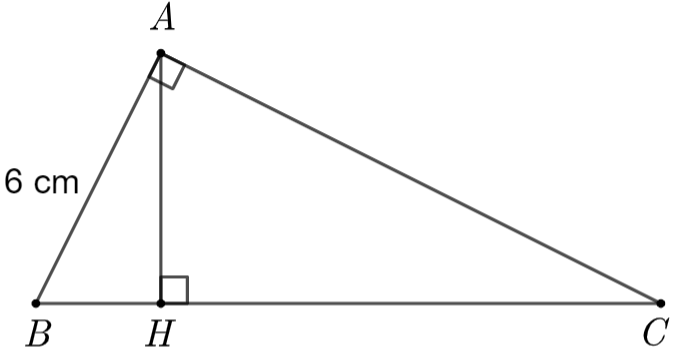
Áp dụng định lí Pythagore, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
\(A{C^2} = B{C^2} - A{B^2} = {10^2} - {6^2} = 64\), suy ra \(AC = 8\,\,{\rm{cm}}\).
Xét \(\Delta ABH\) và \(\Delta CBA\) có \(\widehat {AHB} = \widehat {BAC} = 90^\circ ;\,\,\widehat B\) chung.
Do đó .
Suy ra \(\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\) hay \(A{B^2} = BH\,.\,BC\) nên \(BH = \frac{{A{B^2}}}{{BC}} = \frac{{{6^2}}}{{10}} = 3,6\,\,\left( {{\rm{cm}}} \right)\).
Vậy \(BC = 10\,\,{\rm{cm}},\,\,AC = 8\,\,{\rm{cm}},\,\,BH = 3,6\,\,{\rm{cm}}.\)
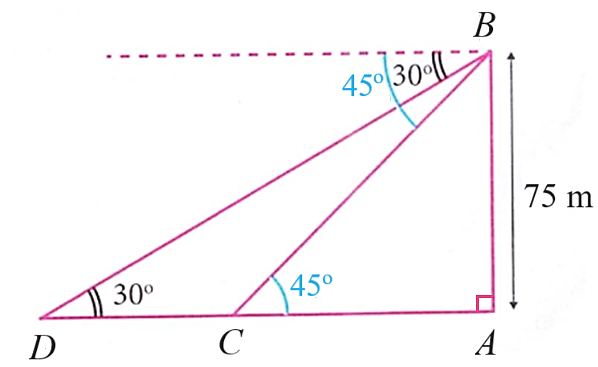
2. Quãng đường chiếc thuyền đi được giữa hai lần quan sát là \(CD.\)
Xét \(\Delta BAC\) vuông tại \(A\) có \(AC = 75\cot \widehat {BCA} = 75\cot 45^\circ = 75\,\,\left( {\rm{m}} \right)\).
Xét \(\Delta DAB\) vuông tại \(A\) có \(AD = 75\cot \widehat {BDA} = 75\cot 30^\circ = 75\sqrt 3 \,\,\left( {\rm{m}} \right)\).
Quãng đường chiếc thuyền đi được giữa hai lần quan sát là:
\(CD = AD - AC = 75\sqrt 3 - 75 \approx 55\,\,\left( {\rm{m}} \right)\).
Vậy chiếc thuyền đi được khoảng 55 mét giữa hai lần quan sát.
Lời giải
Hướng dẫn giải
Ta có: \[{x^2} + 2{y^2} + 2xy + 7x + 7y + 10 = 0.\]
\(\left( {{x^2} + 2xy + {y^2}} \right) + 7x + 7y + {y^2} + 10 = 0\)
\({\left( {x{\rm{ }} + {\rm{ }}y} \right)^2} + 7\left( {x + y} \right) + {y^2} + 10 = 0 & \left( 1 \right)\)
Đặt \[S = x + y\].
Khi đó phương trình \(\left( 1 \right)\) trở thành: \[{S^2} + 7S + {y^2} + 10 = 0\]
\({S^2} + 7S + \frac{{49}}{4} = \frac{9}{4} - {y^2}\)
\({\left( {S + \frac{7}{2}} \right)^2} = \frac{9}{4} - {y^2} \le \frac{9}{4}\).
Dấu xảy ra khi và chỉ khi \(\frac{9}{4} - {y^2} = \frac{9}{4}\) hay \(y = 0\).
Do đó \({\left( {S + \frac{7}{2}} \right)^2} \le \frac{9}{4}\) nên \(\frac{{ - 3}}{2} \le S + \frac{7}{2} \le \frac{3}{2}\) hay \[ - 5 \le S \le - 2.\]
Ta có \(P = \frac{{2x + 2y - 3}}{{x + y + 6}} = \frac{{2\left( {x + y + 6} \right) - 15}}{{x + y + 6}}\) \( = 2 - \frac{{15}}{{x + y + 6}} = 2 - \frac{{15}}{{S + 6}} & \left( 2 \right)\)
Với \[ - \,5 \le S \le - \,2\] thì \(1 \le S + 6 \le 4\)
\(\frac{{15}}{4} \le \frac{{15}}{{S + 6}} \le 15\)
\(2 - 15 \le 2 - \frac{{15}}{{S + 6}} \le 2 - \frac{{15}}{4}\)
\( - 13 \le 2 - \frac{{15}}{{S + 6}} \le - \frac{7}{4}\)
\( - 13 \le P \le - \frac{7}{4}\).
Vậy giá trị nhỏ nhất của biểu thức \[P\] là \[ - 13\] khi \(x = - 5\,;\,\,y = 0\).
Và giá trị lớn nhất của biểu thức \(P\) là \(\frac{{ - 7}}{4}\) khi \[x = - 2\,;\,\,y = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
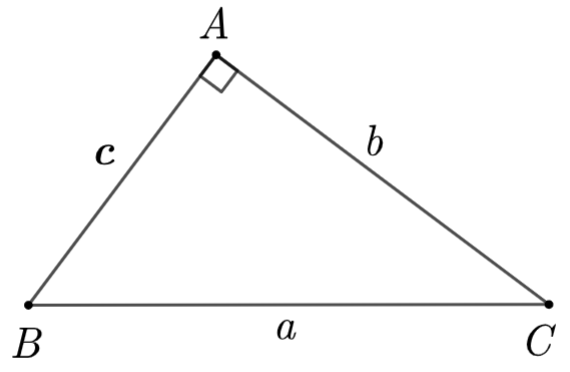
A. \[c = b \cdot \tan B\].
B. \[c = b \cdot \cot C\].
C. \[c = b \cdot \tan C\].
D. \[c = b \cdot \sin B\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
B. \[5x - 3z = 6\].
C. \(5x - 8y = 0.\)
D. \[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[\left( {1\,;\,\, - 2} \right)\].
B. \[\left( {3\,;\,\, - 1} \right)\].
C. \[\left( { - 1\,;\,\, - 3} \right)\].
D. \(\left( {7\,;\,\,1} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.