Câu hỏi:

04/07/2025 118

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. Trong mỗi câu, hãy viết phần trả lời ngắn không quá 4 ký tự (phải là số) và để ngoài MathType

Để đặt được một vật trang trí trên mặt bàn, người ta thiết kế một chân đế như sau. Lấy một khối gỗ có dạng khối chóp cụt tứ giác đều với độ dài hai cạnh đáy lần lượt bằng 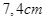và 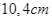, bề dày khối gỗ bằng 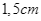. Sau đó khoét bỏ đi một phần của khối gỗ sao cho phần đó có dạng vật thể 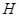, ở đó 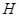nhận được bằng cách cắt khối cầu bán kính 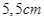bởi một mặt phẳng cắt mà mặt cắt là hình tròn bán kính 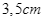(xem hình dưới)

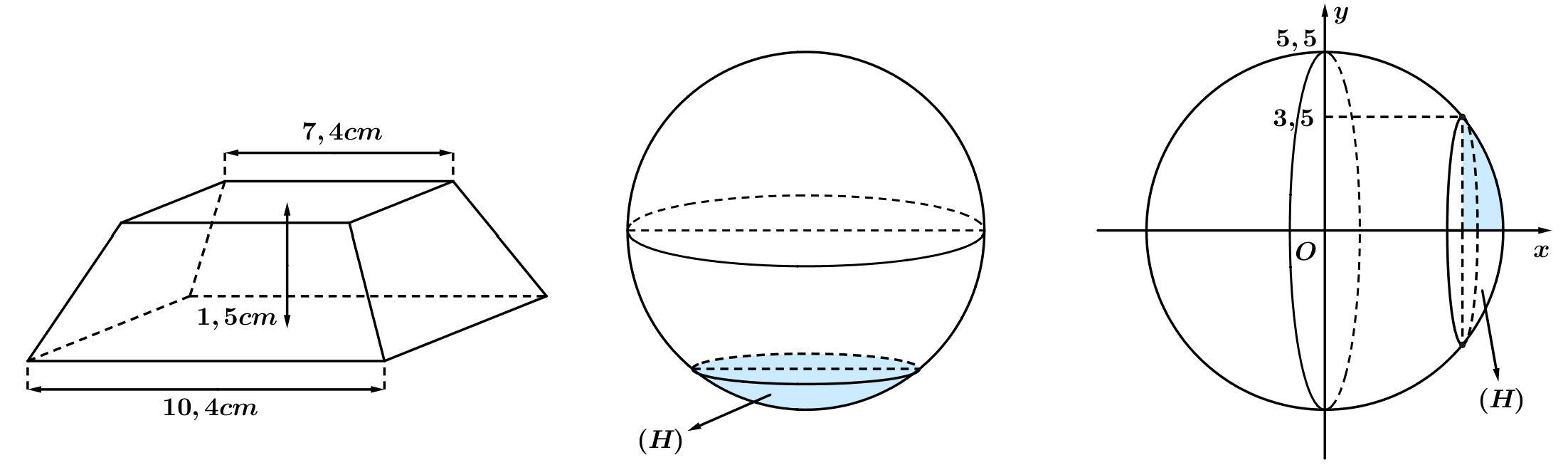
Thể tích của khối chân đế bằng bao nhiêu centimét khối (không làm tròn kết quả các phép tính trung gian, chỉ làm tròn kết quả cuối cùng đến hàng phần mười)

Xem lời giải

Câu hỏi trong đề: Đề chính thức thi Toán Tốt nghiệp 2025 có đáp án (Mã đề 102) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án: 94,7.

Xét trên mặt phẳng tọa độ có đường tròn tâm gốc tọa độ , bán kính là đường tròn thiết diện lớn nhất cắt khối cầu đề cho. Gọi là mặt phẳng đi qua tâm của khối cầu và là mặt phẳng song song với sao cho cách khối cầu 1 khoảng là và biết rằng đường tròn giao tuyến tạo bởi có bán kính bằng .

Khi ấy là nghiệm của phương trình hoành độ giao điểm giữa đường tròn và đường thẳng . Tức ta có phương trình sau:

Nhận thấy vật thể để khoét vào khối chóp cụt có dạng là chỏm cầu có bán kính bằng , khi ấy chiều cao của chỏm này chính bằng (hợp lệ)

Khi ấy thể tích là: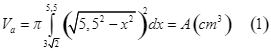

Tại khối chóp cụt, ta thực hiện cắt một mặt phẳng qua đường cao khối chóp và vuông góc với hai đáy, khi ấy ta mô hình hóa được mặt cắt là hình thang vuông như hình vẽ dưới (trong đó lần lượt là tâm mặt đáy bé và đáy lớn của chóp cụt)

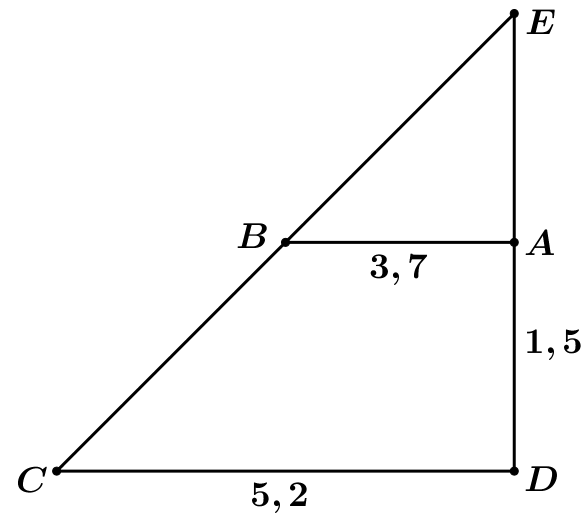
Gọi ,

theo định lí Thales ta có:

Suy ra . Gọi là thể tích khối chóp đều đáy là hình vuông cạnh và đường cao và là thể tích khối chóp đều đáy là hình vuông cạnh và đường cao thì khi ấy thể tích khối chóp cụt bằng:

Từ (1) và (2) ta suy ra thể tích khối chân đế là

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Nếu một doanh nghiệp sản xuất sản phẩm trong một tháng thì doanh thu nhận được khi bán hết số sản phẩm đó là (nghìn đồng), trong khi chi phí sản xuất bình quân cho mỗi sản phẩm là (nghìn đồng). Giả sử số sản phẩm sản xuất ra luôn được bán hết. Trong một tháng, doanh nghiệp đó cần sản xuất ít nhất bao nhiêu sản phẩm để lợi nhuận thu được lớn hơn 100 triệu đồng?

Xem đáp án

Lời giải

Đáp án: 1347.

Lợi nhuận khi bán hết sản phẩm với là:

(nghìn đồng).

Để lợi nhuận thu được lớn hơn triệu đồng (nghìn đồng).

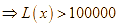
Nếu một doanh nghiệp sản xuất x sản phẩm trong một (ảnh 1)

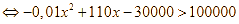Nếu một doanh nghiệp sản xuất x sản phẩm trong một (ảnh 2)

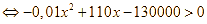
Nếu một doanh nghiệp sản xuất x sản phẩm trong một (ảnh 3)

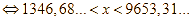
Nếu một doanh nghiệp sản xuất x sản phẩm trong một (ảnh 4)

Giao với điều kiện

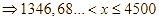
(sản phẩm)

Vậy doanh nghiệp cần sản xuất ít nhất (sản phẩm)

Câu 2

Bạn Nam tham gia cuộc thi giải một mật thư. Theo quy tắc của cuộc thi, người chơi cần chọn ra sáu số từ tập và sắp xếp mỗi số vào đúng một vị trí trong sáu vị trí như hình bên sao cho mỗi vị trí chỉ được sắp xếp một số. Mật thư sẽ được giải nếu các bộ ba số xuất hiện ở những bộ ba vị trí tạo thành các cấp số cộng theo thứ tự đó. Bạn Nam chọn ngẫu nhiên sáu số trong tập và xếp ngẫu nhiên vào các vị trí được yêu cầu. Gọi xác xuất bạn Nam giải được mật khẩu ở lần chọn và xếp đó là . Giá trị bằng bao nhiêu?

Xem đáp án

Lời giải

Đáp án: 2520

Số phần tử của không gian mẫu: (cách).

Gọi là biến cố “Bạn Nam giải được mật khẩu”;

Vì mỗi bộ ba sốlập thành một một cấp số cộng nên: ; ; .

Khi đó bộ ba số phải cùng chẵn hoặc cùng lẻ, ta xét các trường hợp sau:

Trường hợp 1: Bộ ba số cùng chẵn.

Khi đó ta có 2 bộ ba số thỏa mãn là:và , với mỗi cách xếp một bộ ba số vào ba vị trí thì có duy nhất một số được chọn để xếp vào vị trí, một số được chọn để xếp vào vị trí, một số được chọn để xếp vào vị trí.

Số cách Nam giải được mật thư trong trường hợp này là: (cách).

Trường hợp 2: Bộ ba số cùng lẻ.

Khi đó ta có sáu bộ sáu số thỏa mãn là:; , ,,,,với mỗi cách xếp một bộ ba số vào ba vị trí thì có duy nhất một số được chọn để xếp vào vị trí, một số được chọn để xếp vào vị trí, một số được chọn để xếp vào vị trí.