(2,5 điểm)
1. Xác định giá trị của \(a\) và \(b\) để đường thẳng \(y = ax + b\) đi qua hai điểm \(M\left( {3;\,\, - 5} \right)\) và \(N\left( {1;\,\,2} \right).\)
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một số có hai chữ số. Nếu đổi chỗ hai chữ số của nó thì được số mới lớn hơn số đã cho là \(63\). Tổng của số đã cho và số mới tạo thành bằng \(99\). Tìm số đã cho.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
1. Do đường thẳng \(y = ax + b\) đi qua điểm \(M\left( {3;\,\, - 5} \right)\) nên thay \(x = 3,\,\,y = - 5\) vào hàm số \(y = ax + b,\) ta được: \( - 5 = 3a + b\).
Tương tự, do đường thẳng đi qua điểm \(N\left( {1;\,\,2} \right)\) nên ta có: \(2 = a + b\).
Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{3a + b = - 5}\\{a + b = 2}\end{array}} \right.\).
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:
\(2a = - 7,\) suy ra \(a = - \frac{7}{2}\).
Thay \(a = - \frac{7}{2}\) vào phương trình \(a + b = 2\), ta được:
\( - \frac{7}{2} + b = 2,\) suy ra \(b = \frac{{11}}{2}\).
Vậy \(a = - \frac{7}{2}\) và \(b = \frac{{11}}{2}\).
2. Gọi số có hai chữ số cần tìm là \(\overline {xy} {\rm{ }}\left( {x \in \mathbb{N}*,\,\,y \in \mathbb{N}*,\,\,0 < x \le 9,\,\,0 \le y \le 9} \right).\)
Nếu đổi chỗ hai chữ số của nó thì được số mới là \(\overline {yx} \).
Ta có: \(\overline {xy} = 10x + y\) và \(\overline {yx} = 10y + x\).
Theo bài, nếu đổi chỗ hai chữ số của nó thì được số mới lớn hơn số đã cho là \(63\) nên ta có phương trình: \(10y + x = \left( {10x + y} \right) + 63\) hay \( - 9x + 9y = 63\) nên \(x - y = - 7.\) (1)
Mặt khác, tổng của số đã cho và số mới tạo thành bằng \(99\) nên ta có phương trình: \(\left( {10x + y} \right) + \left( {10y + x} \right) = 99\) hay \(11x + 11y = 99\) nên \(x + y = 9.\) (2)
Từ (1) và (2), ta có hệ phương trình: \(\left\{ \begin{array}{l}x - y = - 7\\x + y = 9.\end{array} \right.\)
Cộng từng vế hai phương trình của hệ trên, ta được:
\(2x = 2,\) suy ra \(x = 1\) (thỏa mãn).
Thay \(x = 1\) vào phương trình \(x + y = 9,\) ta được: \(1 + y = 9,\) suy ra \(y = 8\) (thỏa mãn).
Vậy số cần tìm là \(18\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
1. Xét \(\Delta ABD\) vuông tại \(B\), ta có:
⦁ \(\sin C = \frac{{AB}}{{BC}},\) suy ra \(BC = \frac{{AB}}{{\sin C}} = \frac{9}{{\sin 32^\circ }} \approx 16,98.\)
⦁ \(AC = AB \cdot \cot C = 9 \cdot \cot 32^\circ \approx 14,40.\)
Vậy \[AC \approx 14,40\] và \[BC \approx 16,98.\]
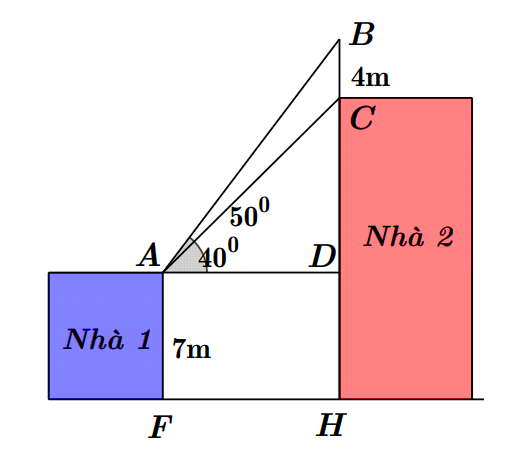
2. Xét \(\Delta ACD\) vuông tại \(D\), ta có: \(DC = AD \cdot \tan \widehat {CAD} = AD \cdot \tan 40^\circ \).
Xét \(\Delta ABD\) vuông tại \(D\), ta có: \(DB = AD \cdot \tan \widehat {BAD} = AD \cdot \tan 50^\circ \).
Ta có: \(BC = DB - DC\)
Suy ra \(4 = AD \cdot \tan 50^\circ - AD \cdot \tan 40^\circ \)
\(4 = AD \cdot \left( {\tan 50^\circ - \tan 40^\circ } \right)\)
\(AD = \frac{4}{{\tan 50^\circ - \tan 40^\circ }}\).
Do đó \(DC = AD \cdot \tan 40^\circ = \frac{{4\tan 40^\circ }}{{\tan 50^\circ - \tan 40^\circ }} \approx 9,5{\rm{\;(m)}}{\rm{.}}\)
Như vậy, \(CH = CD + DH \approx 9,5 + 7 = 16,5{\rm{\;(m)}}{\rm{.}}\)
Vậy chiều cao của tòa nhà 2 khoảng \(16,5{\rm{\;m}}.\)
Câu 2
A. \(BC = \frac{{AC}}{{\sin B}}\).
B. \(BC = \frac{{AB}}{{\sin C}}\).
C. \(BC = \frac{{AC}}{{\cos C}}\).
D. \(AB = \frac{{AC}}{{\tan C}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
|
Xét \(\Delta ABC\) vuông tại \(A\), ta có: ⦁ \(AC = BC \cdot \sin B = BC \cdot \cos C\) nên \(BC = \frac{{AC}}{{\sin B}} = \frac{{AC}}{{\cos C}}\); ⦁ \(AB = BC \cdot \sin C\) nên \(BC = \frac{{AB}}{{\sin C}}\). ⦁ \(\cot C = \frac{{AC}}{{AB}}\) nên \(AB = \frac{{AC}}{{\cot C}}\). Vậy hệ thức ở phương án D là sai. |
|
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(A{B^2} = B{C^2} + A{C^2}\).
B. \(\cot B - \tan B = 0\).
C. \(\sin C = \cos B\).
D. \(\cot C = \frac{{AC}}{{AB}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(5\).
B. \(1\).
C. \( - 5\).
D. \( - 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[ \ge \].
B. \[ \le \].
C. \[ < \].
D. \[ > \].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập