(0,5 điểm) Cho \(a,\,\,b,\,\,c,\,\,d\) là các số thực dương. Chứng minh rằng nếu \(\frac{a}{b} < 1\) thì \(\frac{a}{b} < \frac{{a + c}}{{b + c}}.\,\,\,\left( 1 \right)\)
Áp dụng bất đẳng thức (1) để chứng minh bất đẳng thức sau:
\(1 < \frac{a}{{a + b + c}} + \frac{b}{{b + c + d}} + \frac{c}{{c + d + a}} + \frac{d}{{d + a + b}} < 2\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
⦁ Với \(a,\,\,b,\,\,c\) là các số thực dương, ta có:
\[\frac{{a + c}}{{b + c}} - \frac{a}{b} = \frac{{b\left( {a + c} \right) - a\left( {b + c} \right)}}{{b\left( {b + c} \right)}} = \frac{{ab + bc - ab - ac}}{{b\left( {b + c} \right)}} = \frac{{bc - ac}}{{b\left( {b + c} \right)}} = \frac{{c\left( {b - a} \right)}}{{b\left( {b + c} \right)}}.\]
Theo bài, \(\frac{a}{b} < 1\) nên \(\frac{{b - a}}{b} > 0\) suy ra \(b - a > 0\) (do \(b > 0)\)</>
Do đó \[\frac{{c\left( {b - a} \right)}}{{b\left( {b + c} \right)}} > 0\] với mọi số thực dương \(a,\,\,b,\,\,c\) thỏa mãn \(\frac{a}{b} < 1.\)
Như vậy, bất đẳng thức \(\frac{a}{b} < \frac{{a + c}}{{b + c}}\,\,\,\left( 1 \right)\) được chứng minh.
⦁ Với \(a,\,\,b,\,\,c\) là các số thực dương, ta có: \(\frac{a}{{a + b + c}} < 1\).
Áp dụng bất đẳng thức (1) ta được \(\frac{a}{{a + b + c}} < \frac{{a + d}}{{a + b + c + d}}.\)
Tương tự, ta có: \(\frac{b}{{b + c + d}} < \frac{{b + a}}{{a + b + c + d}};\,\,\,\frac{c}{{c + d + a}} < \frac{{c + b}}{{a + b + c + d}};\,\,\,\frac{d}{{d + a + b}} < \frac{{d + a}}{{a + b + c + d}}.\)
Suy ra
\(\frac{a}{{a + b + c}} + \frac{b}{{b + c + d}} + \frac{c}{{c + d + a}} + \frac{d}{{d + a + b}} < \frac{{a + d}}{{a + b + c + d}} + \frac{{b + a}}{{a + b + c + d}} + \frac{{c + b}}{{a + b + c + d}} + \frac{{d + a}}{{a + b + c + d}}\)
Do đó \(\frac{a}{{a + b + c}} + \frac{b}{{b + c + d}} + \frac{c}{{c + d + a}} + \frac{d}{{d + a + b}} < \frac{{2\left( {a + b + c + d} \right)}}{{a + b + c + d}} = 2\). (2)
⦁ Với \(a,\,\,b,\,\,c\) là các số thực dương, ta có: \(a + b + c < a + b + c + d\) nên \(\frac{a}{{a + b + c}} > \frac{a}{{a + b + c + d}}\).</>
Tương tự, ta có \(\frac{b}{{b + c + d}} > \frac{b}{{a + b + c + d}};\,\,\,\frac{c}{{c + d + a}} > \frac{c}{{a + b + c + d}};\,\,\,\frac{d}{{d + a + b}} > \frac{d}{{a + b + c + d}}.\)
Suy ra
\(\frac{a}{{a + b + c}} + \frac{b}{{b + c + d}} + \frac{c}{{c + d + a}} + \frac{d}{{d + a + b}} > \frac{a}{{a + b + c + d}} + \frac{b}{{a + b + c + d}} + \frac{c}{{a + b + c + d}} + \frac{d}{{a + b + c + d}}\)
Do đó \(\frac{a}{{a + b + c}} + \frac{b}{{b + c + d}} + \frac{c}{{c + d + a}} + \frac{d}{{d + a + b}} > \frac{{a + b + c + d}}{{a + b + c + d}} = 1\). (3)
Từ (2) và (3) suy ra \(1 < \frac{a}{{a + b + c}} + \frac{b}{{b + c + d}} + \frac{c}{{c + d + a}} + \frac{d}{{d + a + b}} < 2\).
Như vậy bất đẳng thức \(1 < \frac{a}{{a + b + c}} + \frac{b}{{b + c + d}} + \frac{c}{{c + d + a}} + \frac{d}{{d + a + b}} < 2\) đã được chứng minh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
1. Xét \(\Delta ABD\) vuông tại \(B\), ta có:

⦁ \(\sin C = \frac{{AB}}{{BC}},\) suy ra \(BC = \frac{{AB}}{{\sin C}} = \frac{9}{{\sin 32^\circ }} \approx 16,98.\)
⦁ \(AC = AB \cdot \cot C = 9 \cdot \cot 32^\circ \approx 14,40.\)
Vậy \[AC \approx 14,40\] và \[BC \approx 16,98.\]
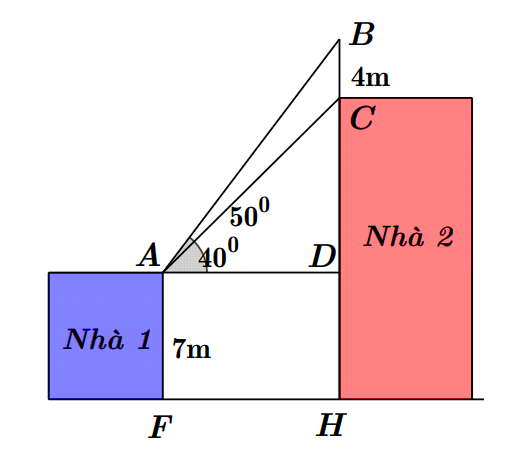
2. Xét \(\Delta ACD\) vuông tại \(D\), ta có: \(DC = AD \cdot \tan \widehat {CAD} = AD \cdot \tan 40^\circ \).
Xét \(\Delta ABD\) vuông tại \(D\), ta có: \(DB = AD \cdot \tan \widehat {BAD} = AD \cdot \tan 50^\circ \).
Ta có: \(BC = DB - DC\)
Suy ra \(4 = AD \cdot \tan 50^\circ - AD \cdot \tan 40^\circ \)
\(4 = AD \cdot \left( {\tan 50^\circ - \tan 40^\circ } \right)\)
\(AD = \frac{4}{{\tan 50^\circ - \tan 40^\circ }}\).
Do đó \(DC = AD \cdot \tan 40^\circ = \frac{{4\tan 40^\circ }}{{\tan 50^\circ - \tan 40^\circ }} \approx 9,5{\rm{\;(m)}}{\rm{.}}\)
Như vậy, \(CH = CD + DH \approx 9,5 + 7 = 16,5{\rm{\;(m)}}{\rm{.}}\)
Vậy chiều cao của tòa nhà 2 khoảng \(16,5{\rm{\;m}}.\)
Câu 2
A. \(BC = \frac{{AC}}{{\sin B}}\).
B. \(BC = \frac{{AB}}{{\sin C}}\).
C. \(BC = \frac{{AC}}{{\cos C}}\).
D. \(AB = \frac{{AC}}{{\tan C}}\).
Lời giải
Đáp án đúng là: D
|
Xét \(\Delta ABC\) vuông tại \(A\), ta có: ⦁ \(AC = BC \cdot \sin B = BC \cdot \cos C\) nên \(BC = \frac{{AC}}{{\sin B}} = \frac{{AC}}{{\cos C}}\); ⦁ \(AB = BC \cdot \sin C\) nên \(BC = \frac{{AB}}{{\sin C}}\). ⦁ \(\cot C = \frac{{AC}}{{AB}}\) nên \(AB = \frac{{AC}}{{\cot C}}\). Vậy hệ thức ở phương án D là sai. |
|
Câu 3
A. \(A{B^2} = B{C^2} + A{C^2}\).
B. \(\cot B - \tan B = 0\).
C. \(\sin C = \cos B\).
D. \(\cot C = \frac{{AC}}{{AB}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(5\).
B. \(1\).
C. \( - 5\).
D. \( - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(2x + 1 > \left( {2x + 4} \right)x\).
B. \(\frac{{2x}}{3} - 2 < 0\).
C. \(0x - 4 \ge - 4\).
D. \({x^2} + 2x + 1 \ge 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.