Cặp số nào sau đây là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}3x + 4y = 42\\10x - 9y = 6\end{array} \right.?\]

Hướng dẫn giải

Gọi vận tốc của ô tô và vận tốc của xe máy lần lượt là \(x,y{\rm{ }}\left( {{\rm{km/h}}} \right)\) và \(x,y > 0.\)

Sau 2 giờ ô tô đi được quãng đường là \(2x{\rm{ }}\left( {{\rm{km}}} \right)\).

Sau 2 giờ xe máy đi được quãng đường là \(2y{\rm{ }}\left( {{\rm{km}}} \right)\)

Vì hai xe khởi hành cùng một lúc từ hai tỉnh cách nhau \(200{\rm{ km,}}\) đi ngược chiều và gặp nhau sau 2 giờ nên ta có phương trình \[2x + 2y = 200\] hay \[x + y = 100 & \left( 1 \right)\]

Nếu vận tốc của ô tô tăng thêm \(10{\rm{ km/h}}\) thì vận tốc mới của ô tô là: \(x + 10{\rm{ }}\left( {{\rm{km/h}}} \right)\).

Nếu vận tốc của xe máy giảm đi \({\rm{5 km/h}}\) thì vận tốc mới của xe máy là \(y - 5{\rm{ }}\left( {{\rm{km/h}}} \right)\).

Vì vận tốc của ô tô tăng thêm \(10{\rm{ km/h}}\) và vận tốc của xe máy giảm đi \({\rm{5 km/h}}\) thì lúc này vận tốc của ô tô bằng 2 lần vận tốc của xe máy nên ta có phương trình

\(x + 10 = 2\left( {y - 5} \right)\) hay \(x - 2y = - 20 & \left( 2 \right)\).

Từ \[\left( 1 \right)\] và \(\left( 2 \right)\) ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 100\\x - 2y = - 20\end{array} \right.\).

Trừ từng vế hai phương trình của hệ trên, ta được: \(3y = 120\), suy ra \(y = 40\) (thỏa mãn).

Thay \(y = 40\) vào phương trình \(x + y = 100\), ta được:

\(x + 40 = 100\) suy ra \(x = 60\) (thỏa mãn).

Vậy vận tốc của ô tô là \(60{\rm{ km/h}}\) và vận tốc của xe máy là \(40{\rm{ km/h}}\).

Hướng dẫn giải

1.  Xét tam giác \(ABH\) vuông tại \(H\), ta có:

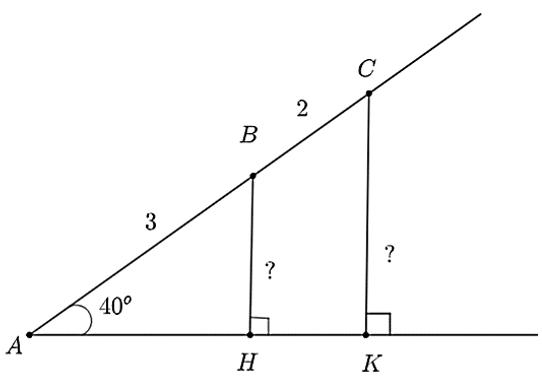
\(\sin A = \frac{{BH}}{{AH}}\) suy ra \(BH = AH.\sin A = 3.\sin 40^\circ \approx 1,9.\)

Xét tam giác \(ACK\) vuông tại \(K\), ta có:

\(AC = AB + BC = 3 + 2 = 5\).

\(\sin A = \frac{{CK}}{{AC}}\) suy ra \(CK = AC.\sin A = 5.\sin 40^\circ \approx 3,2\).

Xét tam giác \(ACK\) vuông tại \(K\), ta có:

\(\tan A = \frac{{CK}}{{AK}}\) suy ra \(AK = \frac{{CK}}{{\tan A}} = \frac{{3,2}}{{\tan 40^\circ }} \approx 3,8.\)

Vậy \(BH \approx 1,9\), \(CK \approx 3,2\), \(AK \approx 3,8.\)

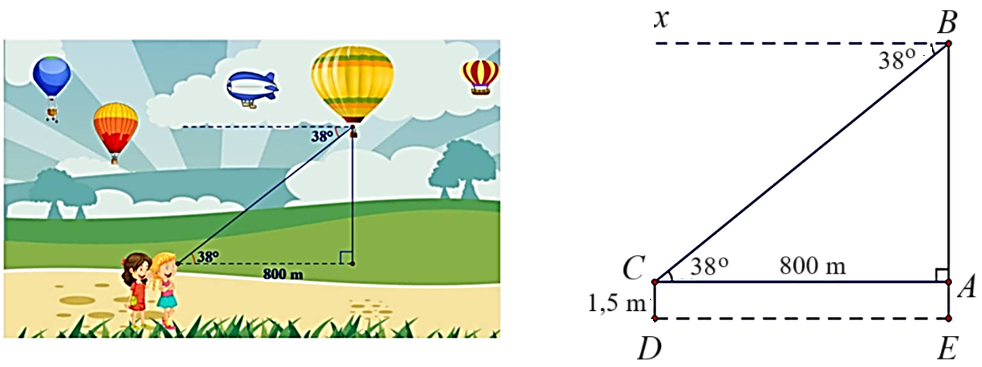
2. Quan sát hình vẽ hình học của bài toán, ta có:

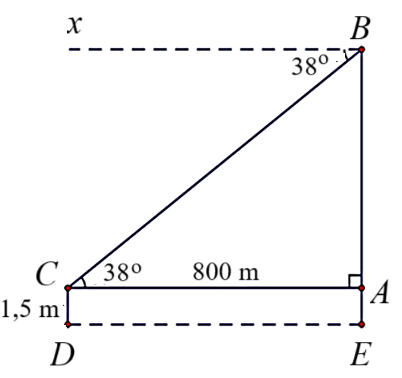
Độ cao của khinh khí cầu so với mặt đất là đoạn thẳng \(BE.\)

Xét tam giác \(ABC\) vuông tại \(A\), ta có:

\(\tan \widehat {BCA} = \frac{{AB}}{{AC}}\) hay \(AB = AC.\tan \widehat {BCA}\).

Suy ra \[AB = 800.\tan 38^\circ \approx 625\,\,\left( {\rm{m}} \right)\].

Ta có \(BE = AB + AE \approx 625 + 1,5 = 626,5\,\,\left( {\rm{m}} \right)\).

Vậy độ cao của khinh khí cầu so với mặt đất khoảng \(626,5\,\,{\rm{m}}{\rm{.}}\)