Trong các số dưới đây, số nào là số vô tỉ?
A. \(0,3.\)
B. \( - 1,\left( 1 \right).\)
C. \(\sqrt 5 .\)
D. \(\sqrt 4 .\)
Quảng cáo
Trả lời:
Đáp án đúng là: C
Nhận thấy:
• \(0,3\) là số hữu tỉ.
• \( - 1,\left( 1 \right)\) là số thập phân vô hạn tuần hoàn.
• \(\sqrt 5 \) là số vô tỉ.
• \(\sqrt 4 = \sqrt {{2^2}} = 2\) là số hữu tỉ.
Do đó, chọn đáp án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 (chương trình mới) ( 120.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Học sinh vẽ lại hình theo đúng số đo các góc.
|
GT |
\(\widehat {xAB} = 30^\circ ,\widehat {HBz} = 150^\circ ,AH \bot mn;\) tia phân giác \(Av\) của \(\widehat {HAt}\) |
|
KL |
b) \(xy\parallel mn.\) c) \(AH\) là tia phân giác của \(\widehat {BAv}.\) |
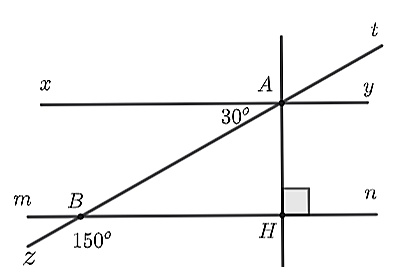
b) Nhận thấy \(\widehat {zBH}\) và \(\widehat {ABH}\) là hai góc kề bù nên ta có: \(\widehat {zBH} + \widehat {ABH} = 180^\circ \) hay \(150^\circ + \widehat {ABH} = 180^\circ .\)
Suy ra \(\widehat {ABH} = 180^\circ - 150^\circ = 30^\circ \).
Do đó, \(\widehat {ABH} = \widehat {BAx} = 30^\circ \).
Mà hai góc ở vị trí so le trong nên \(xy\parallel mn.\)
c)
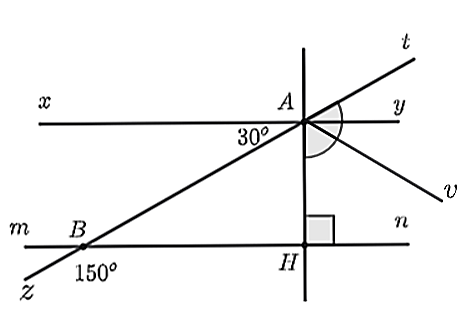
Ta có \(xy\parallel mn\) và \(AH \bot mn\) nên \(AH \bot xy\).
Do đó, \(\widehat {xAH} = 90^\circ \).
Ta có \(\widehat {xAB}\) và \(\widehat {BAH}\) là hai góc kề nhau nên \(\widehat {xAB} + \widehat {BAH} = \widehat {xAH}\),
Do đó \(\widehat {BAH} = \widehat {xAH} - \widehat {xAB} = 90^\circ - 30^\circ = 60^\circ \).
Lại có \(\widehat {BAH}\) và \(\widehat {HAt}\) là hai góc kề bù nên \(\widehat {BAH} + \widehat {HAt} = 180^\circ \)
hay \(\widehat {HAt} = 180^\circ - \widehat {BAH} = 180^\circ - 60^\circ = 120^\circ .\)
Mà \(Av\) là tia phân giác của \(\widehat {HAt}\) nên \(\widehat {HAv} = \widehat {vAt} = \widehat {\frac{{HAt}}{2}} = \frac{{120^\circ }}{2} = 60^\circ \).
Nhận thấy \(\widehat {HAv} = \widehat {HAB} = 60^\circ \), đồng thời tia \(AH\) nằm giữa hai tia \(AB,Av\).
Do đó, \(AH\) là tia phân giác của \(\widehat {BAv}.\)
Lời giải
Hướng dẫn giải
Đáp án: \(1,5\)
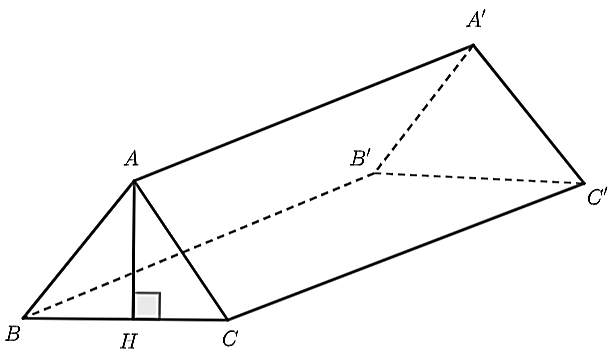
Diện tích đáy của lều là: \(2,16:2,4 = 0,9{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Chiều cao \(AH\) của lều là: \(2.0,9:1,2 = 1,5{\rm{ }}\left( {\rm{m}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \( - \frac{4}{3}.\)
B. \(\frac{4}{3}.\)
C. \(\frac{3}{4}.\)
D. \( - \frac{3}{4}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.