Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Một cửa hàng điện máy nhập về 100 chiếc máy tính xách tay với giá 8 triệu đồng một chiếc. Sau khi đã bán được \(70\) chiếc với tiền lãi bằng \(30\% \) giá vốn, số máy còn lại được bán với mức giá bằng \(65\% \) giá bán trước đó.
a) Giá vốn cửa hàng bỏ ra khi nhập về 100 chiếc máy tính là \(800\) triệu đồng.
b) Cửa hàng bán 70 chiếc máy đầu với giá bằng \(130\% \) so với giá vốn.
c) Giá tiền bán 30 chiếc máy tính còn lại nhỏ hơn \(200\) triệu đồng.
d) Sau khi bán hết, cửa hàng đã lãi hơn \(130\) triệu đồng.
Câu hỏi trong đề: Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: a) Đ b) Đ c) S d) Đ
• Giá vốn cửa hàng bỏ ra khi nhập về 100 chiếc máy tính là: \(8.100 = 800\) (triều đồng).
Do đó, ý a) là đúng.
• Vì cửa hàng đã bán 70 chiếc với tiền lãi bằng \(30\% \) giá vốn nên 70 chiếc máy tính đầu bán với giá bằng \(100\% + 30\% = 130\% \) so với giá vốn.
Do đó, ý b) là đúng.
• Giá tiền bán 70 chiếc máy tính là: \(70.8.130\% = 728\) (triệu đồng)
Vì cửa hàng bán số máy còn lại với mức giá bằng \(65\% \) giá bán trước đó, tức là bán 30 chiếc máy tính còn lại, giá bán mỗi chiếc bằng \(130\% .65\% = 84,5\% \) so với giá mua.
Vậy số tiền cửa hàng thu về khi bán 30 chiếc máy tính còn lại là:
\(30.8.64,5\% = 202,8\) (triệu đồng)
Do đó, ý c) là sai.
• Số tiền cửa hàng thu về khi bán 100 chiếc máy tính đó là: \(728 + 202,8 = 930,8\) (triệu đồng).
Do đó, cửa hàng lãi số tiền là: \(930,8 - 800 = 130,8\) (triệu đồng).
Do đó, ý d) là sai.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Học sinh vẽ lại hình theo đúng số đo các góc.
|
GT |
\(\widehat {xAB} = 30^\circ ,\widehat {HBz} = 150^\circ ,AH \bot mn;\) tia phân giác \(Av\) của \(\widehat {HAt}\) |
|
KL |
b) \(xy\parallel mn.\) c) \(AH\) là tia phân giác của \(\widehat {BAv}.\) |
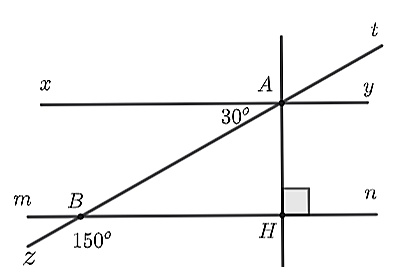
b) Nhận thấy \(\widehat {zBH}\) và \(\widehat {ABH}\) là hai góc kề bù nên ta có: \(\widehat {zBH} + \widehat {ABH} = 180^\circ \) hay \(150^\circ + \widehat {ABH} = 180^\circ .\)
Suy ra \(\widehat {ABH} = 180^\circ - 150^\circ = 30^\circ \).
Do đó, \(\widehat {ABH} = \widehat {BAx} = 30^\circ \).
Mà hai góc ở vị trí so le trong nên \(xy\parallel mn.\)
c)
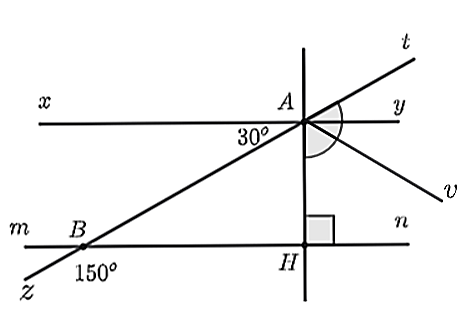
Ta có \(xy\parallel mn\) và \(AH \bot mn\) nên \(AH \bot xy\).
Do đó, \(\widehat {xAH} = 90^\circ \).
Ta có \(\widehat {xAB}\) và \(\widehat {BAH}\) là hai góc kề nhau nên \(\widehat {xAB} + \widehat {BAH} = \widehat {xAH}\),
Do đó \(\widehat {BAH} = \widehat {xAH} - \widehat {xAB} = 90^\circ - 30^\circ = 60^\circ \).
Lại có \(\widehat {BAH}\) và \(\widehat {HAt}\) là hai góc kề bù nên \(\widehat {BAH} + \widehat {HAt} = 180^\circ \)
hay \(\widehat {HAt} = 180^\circ - \widehat {BAH} = 180^\circ - 60^\circ = 120^\circ .\)
Mà \(Av\) là tia phân giác của \(\widehat {HAt}\) nên \(\widehat {HAv} = \widehat {vAt} = \widehat {\frac{{HAt}}{2}} = \frac{{120^\circ }}{2} = 60^\circ \).
Nhận thấy \(\widehat {HAv} = \widehat {HAB} = 60^\circ \), đồng thời tia \(AH\) nằm giữa hai tia \(AB,Av\).
Do đó, \(AH\) là tia phân giác của \(\widehat {BAv}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
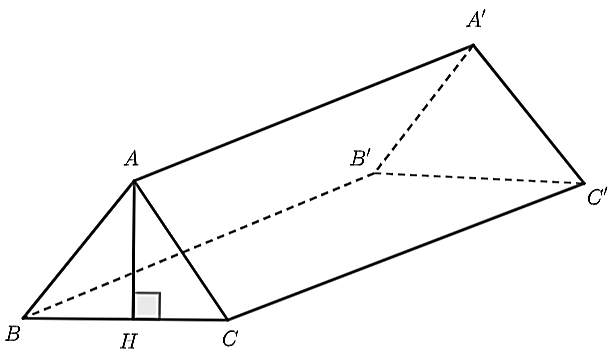
Đáp án: \(1,5\)
Diện tích đáy của lều là: \(2,16:2,4 = 0,9{\rm{ }}\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Chiều cao \(AH\) của lều là: \(2.0,9:1,2 = 1,5{\rm{ }}\left( {\rm{m}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{a}{2} = \frac{b}{3} = \frac{c}{5}.\)
B. \(\frac{a}{5} = \frac{b}{3} = \frac{c}{2}.\)
C. \(\frac{a}{3} = \frac{b}{5} = \frac{c}{2}.\)
D. \(\frac{a}{2} = \frac{b}{5} = \frac{c}{3}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập