Trong các số sau đây, số nào viết được dưới dạng số thập phân vô hạn tuần hoàn?

Hướng dẫn giải

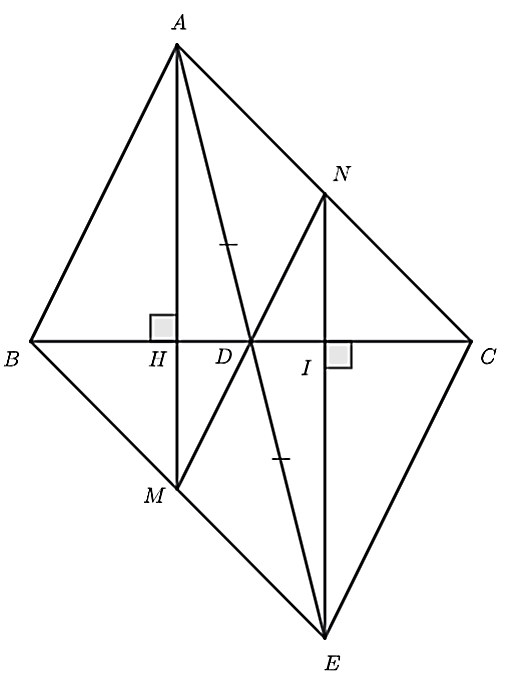
a) Xét \(\Delta ADB\) và \(\Delta EDC\), có:

\(AD = DE\) (gt)

\(\widehat {ADB} = \widehat {CDE}\) (đối đỉnh)

\(BD = DC\) (gt)

Do đó, \(\Delta ADB = \Delta EDC\) (c.g.c)

b) Xét \(\Delta ADC\) và \(\Delta EDB\), có:

\(AD = DE\) (gt)

\(\widehat {ADC} = \widehat {BDE}\) (đối đỉnh)

\(BD = DC\) (gt)

Do đó, \(\Delta ADC = \Delta EDB\) (c.g.c)

Suy ra \(\widehat {BED} = \widehat {DAC}\) (hai góc tương ứng).

Mà hai góc ở vị trí so le trong nên \(AC\parallel BE.\)

c) Xét \(\Delta HBA\) và \(\Delta ICE\), có:

\(AB = EC{\rm{ }}\left( {\Delta ADB = \Delta EDC} \right)\)

\(\widehat {AHB} = \widehat {EIC} = 90^\circ \) (gt)

\(\widehat {ABH} = \widehat {ICE}{\rm{ }}\left( {\Delta ADB = \Delta EDC} \right)\)

Do đó, \(\Delta HBA = \Delta ICE\) (ch – gn)

Suy ra \(BH = IC\) (hai cạnh tương ứng).

Xét \(\Delta HBM\) và \(\Delta ICN,\) có:

\(BH = IC\) (cmt)

\(\widehat {BHM} = \widehat {NIC} = 90^\circ \) (gt)

\(\widehat {MBH} = \widehat {ICN}\) (so le trong)

Do đó, \(\Delta HBM = \Delta ICN\) (cgv – gn)

Suy ra \(BM = NC\) (hai cạnh tương ứng)

Xét \(\Delta BDM\) và \(\Delta CDN\), có:

\(BM = CN\) (cmt)

\(BD = DC\) (gt)

\(\widehat {MBD} = \widehat {DCN}\) (so le trong)

Do đó, \(\Delta BDM = \Delta CDN\) (c.g.c)

Suy ra \(\widehat {BDM} = \widehat {CDN}\) (hai cạnh tương ứng)

Ta có, \(\widehat {BDM}\) và \(\widehat {CDM}\) là hai góc kề bù nên \(\widehat {BDM} + \widehat {CDM} = 180^\circ \).

Mà \(\widehat {BDM} = \widehat {CDN}\) (cmt) suy ra \(\widehat {CDN} + \widehat {CDM} = 180^\circ \) hay \(\widehat {NDM} = 180^\circ \).

Suy ra ba điểm \(D,M,N\) thẳng hàng.

Hướng dẫn giải

Đáp án đúng là:

a) S

b) Đ

c) Đ

d) Đ

Nhận thấy,

• \(\widehat {aAx'}\) và \(\widehat {ABC}\) là hai góc đồng vị. Do đó, ý a) là sai.

• Ta có: \(\widehat {aAx'} = \widehat {ABC} = 60^\circ \), đồng thời hai góc ở vị trí đồng vị nên \(x'x\parallel yy'.\) Do đó, ý b) là đúng.

• Có \(\widehat {aAx'}\) và \(\widehat {BAx'}\) nên \(\widehat {aAx'} + \widehat {BAx'} = 180^\circ \), suy ra \(\widehat {BAx'} = 180^\circ - \widehat {aAx'} = 180^\circ - 60^\circ = 120^\circ \).

Do đó, ý c) là đúng.

• Có tia \(AC\) là tia phân giác của \(\widehat {BAx'}\) nên \(\widehat {BAC} = \widehat {CAx'} = \frac{{\widehat {BAx'}}}{2} = 60^\circ \).

Ta có \(x'x\parallel yy'\) nên \(\widehat {BAx} = \widehat {ABC} = 60^\circ \) (so le trong).

Suy ra \(\widehat {BAx} = \widehat {BAC} = 60^\circ \).

Mà tia \(AB\) nằm trong \(\widehat {xAC}\) nên \(AB\) là tia phân giác của \(\widehat {xAC}\). Do đó, ý d) là đúng.