Một định lí gồm
A. Giả thiết và định nghĩa.
B. Định nghĩa và kết luận.
C. Giả thiết và kết luận.
D. Định nghĩa và chứng minh.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Một định lí gồm giả thiết và kết luận.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
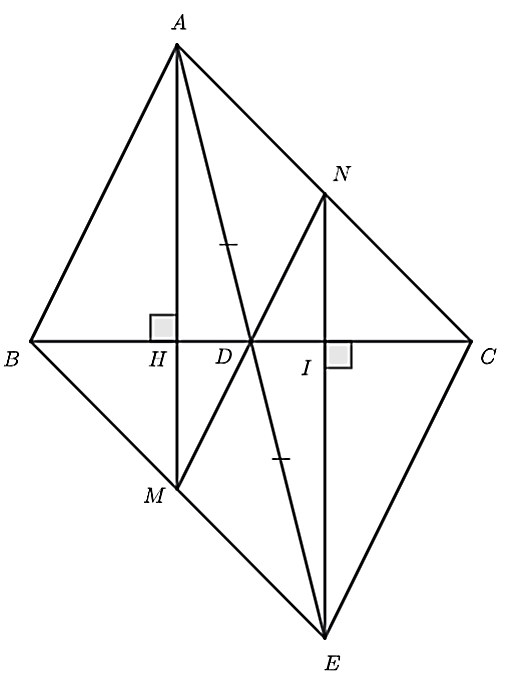
a) Xét \(\Delta ADB\) và \(\Delta EDC\), có:
\(AD = DE\) (gt)
\(\widehat {ADB} = \widehat {CDE}\) (đối đỉnh)
\(BD = DC\) (gt)
Do đó, \(\Delta ADB = \Delta EDC\) (c.g.c)
b) Xét \(\Delta ADC\) và \(\Delta EDB\), có:
\(AD = DE\) (gt)
\(\widehat {ADC} = \widehat {BDE}\) (đối đỉnh)
\(BD = DC\) (gt)
Do đó, \(\Delta ADC = \Delta EDB\) (c.g.c)
Suy ra \(\widehat {BED} = \widehat {DAC}\) (hai góc tương ứng).
Mà hai góc ở vị trí so le trong nên \(AC\parallel BE.\)
c) Xét \(\Delta HBA\) và \(\Delta ICE\), có:
\(AB = EC{\rm{ }}\left( {\Delta ADB = \Delta EDC} \right)\)
\(\widehat {AHB} = \widehat {EIC} = 90^\circ \) (gt)
\(\widehat {ABH} = \widehat {ICE}{\rm{ }}\left( {\Delta ADB = \Delta EDC} \right)\)
Do đó, \(\Delta HBA = \Delta ICE\) (ch – gn)
Suy ra \(BH = IC\) (hai cạnh tương ứng).
Xét \(\Delta HBM\) và \(\Delta ICN,\) có:
\(BH = IC\) (cmt)
\(\widehat {BHM} = \widehat {NIC} = 90^\circ \) (gt)
\(\widehat {MBH} = \widehat {ICN}\) (so le trong)
Do đó, \(\Delta HBM = \Delta ICN\) (cgv – gn)
Suy ra \(BM = NC\) (hai cạnh tương ứng)
Xét \(\Delta BDM\) và \(\Delta CDN\), có:
\(BM = CN\) (cmt)
\(BD = DC\) (gt)
\(\widehat {MBD} = \widehat {DCN}\) (so le trong)
Do đó, \(\Delta BDM = \Delta CDN\) (c.g.c)
Suy ra \(\widehat {BDM} = \widehat {CDN}\) (hai cạnh tương ứng)
Ta có, \(\widehat {BDM}\) và \(\widehat {CDM}\) là hai góc kề bù nên \(\widehat {BDM} + \widehat {CDM} = 180^\circ \).
Mà \(\widehat {BDM} = \widehat {CDN}\) (cmt) suy ra \(\widehat {CDN} + \widehat {CDM} = 180^\circ \) hay \(\widehat {NDM} = 180^\circ \).
Suy ra ba điểm \(D,M,N\) thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
|
a) \(27\frac{1}{5}.\frac{3}{8} - 3\frac{1}{5}:\frac{8}{3}\) \( = 27\frac{1}{5}.\frac{3}{8} - 3\frac{1}{5}.\frac{3}{8}\) \( = \left( {27\frac{1}{5} - 3\frac{1}{5}} \right).\frac{3}{8}\) \( = \left( {27 + \frac{1}{5} - 3 - \frac{1}{5}} \right).\frac{3}{8}\) \( = 24.\frac{3}{8}\) \( = 9.\) |
b) \({\left( {1 - \frac{1}{2}} \right)^2} + \left| { - \frac{3}{5}} \right|.\sqrt {\frac{1}{{16}}} - \left( { - \frac{2}{5}} \right):{2^2}\) \( = {\left( {\frac{1}{2}} \right)^2} + \left| { - \frac{3}{5}} \right|.\sqrt {{{\left( {\frac{1}{4}} \right)}^2}} - \left( { - \frac{2}{5}} \right):4\) \( = \frac{1}{4} + \frac{3}{5}.\frac{1}{4} + \frac{2}{5}.\frac{1}{4}\) \( = \left( {1 + \frac{3}{5} + \frac{2}{5}} \right).\frac{1}{4}\) \( = 2.\frac{1}{4}\) \( = \frac{1}{2}.\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(345,68.\)
B. \(345,7.\)
C. \(350.\)
D. \(346.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Học sinh khối 7 của một trường THCS có \(200\) học sinh đăng kí thực đơn ăn trưa và được biểu diễn bằng bảng số liệu dưới đây.
|
Món ăn |
Pizza |
Mì ý |
Hamburger |
Donut |
|
Tỉ lệ học sinh |
12,5% |
30% |
50% |
7,5% |
Hỏi có bao nhiêu học sinh đăng kí ăn Pizza và Mì ý?
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập