Cho biểu đồ sau:

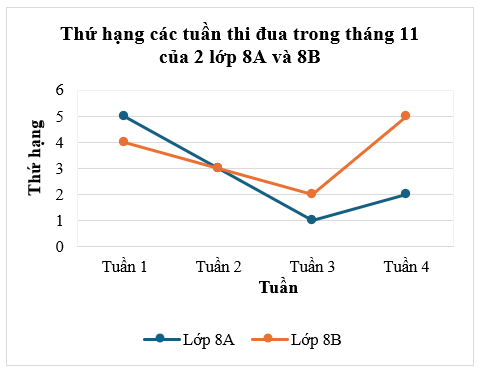
Hỏi tuần nào mà hai lớp 8A và 8B có cùng thứ hạng thi đua?

Hướng dẫn giải

Đáp số: \[ - {\bf{8}}\].

Ta có \[T = \left( {{x^2} - 6x + 12} \right)\left( {x - 6} \right) - {\left( {x - 4} \right)^3}\]

\[ = {x^3} - 6{x^2} + 12x - 6{x^2} + 36x - 72 - \left( {{x^3} - 12{x^2} + 48x - 64} \right)\]

\[ = {x^3} - 12{x^2} + 48x - 72 - {x^3} + 12{x^2} - 48x + 64\]

\( = \left( {{x^3} - {x^3}} \right) + \left( {12{x^2} - 12{x^2}} \right) + \left( {48x - 48x} \right) + \left( {64 - 72} \right)\)\( = - 8\).

Vậy \(T = - 8.\)

Hướng dẫn giải

Ta có \({a^2} + {b^2} + {c^2} = ab + bc + ca\)

\(2{a^2} + 2{b^2} + 2{c^2} = 2ab + 2bc + 2ca\)

\(2{a^2} + 2{b^2} + 2{c^2} - 2ab - 2bc - 2ca = 0\)

\(\left( {{a^2} - 2ab + {b^2}} \right) + \left( {{b^2} - 2bc + {c^2}} \right) + \left( {{c^2} - 2ac + {a^2}} \right) = 0\)

\({\left( {a - b} \right)^2} + {\left( {b - c} \right)^2} + {\left( {c - a} \right)^2} = 0\) (*)

Với mọi \(a,\,\,b,\,\,c \in \mathbb{R}\), ta có: \({\left( {a - b} \right)^2} \ge 0\,;\,\,\,{\left( {b - c} \right)^2} \ge 0\,;\,\,{\left( {c - a} \right)^2} \ge 0\).

Khi đó, \({\left( {a - b} \right)^2} + {\left( {b - c} \right)^2} + {\left( {c - a} \right)^2} \ge 0\).

Do đó để (*) xảy ra thì \[\left\{ \begin{array}{l}{\left( {a - b} \right)^2} = 0\\{\left( {b - c} \right)^2} = 0\\{\left( {c - a} \right)^2} = 0\end{array} \right.\] hay \[\left\{ \begin{array}{l}a - b = 0\\b - c = 0\\c - a = 0\end{array} \right.\] tức là \[\left\{ \begin{array}{l}a = b\\b = c\\c = a\end{array} \right.\].

Khi đó \[a = b = c\] và \(a + b + c = 2025\)

Do đó \[a = b = c = \frac{{2\,\,025}}{3} = 675.\]