Cho hình thang ABCD có AB // CD . Lấy I là trung điểm của DC. Từ I kẻ IM // AC (M = AD) và IN // BD (N = BC)
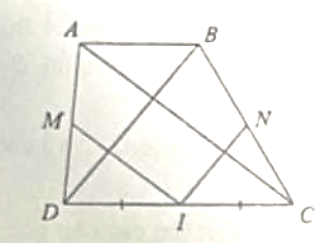
a) Chứng minh 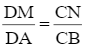
b) Chứng minh MI.BD = IN.AC
Cho hình thang ABCD có AB // CD . Lấy I là trung điểm của DC. Từ I kẻ IM // AC (M = AD) và IN // BD (N = BC)

a) Chứng minh 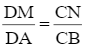
b) Chứng minh MI.BD = IN.AC
Quảng cáo
Trả lời:
a) Vì I là trung điểm DC nên DI = CI = ![]()
Xét tam giác ADC có IM // AC nên theo Ta-lét ta có:
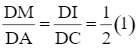
IN // BD ⇒ 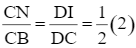
Từ (1) và (2) suy ra: 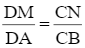
b) IM // AC nên 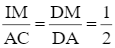
IN // BD nên 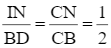
Suy ra: 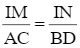
Vậy MI.BD = IN.AC.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Điều kiện: m + 1 ≤ 2m – 1 ⇒ m ≥ 2
Để A là tập con của B thì ![Cho 2 tập hợp A = [m + 1; 2m - 1], B = (0;6) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid34-1753184288.png)
Suy ra: ![]()
Kết hợp với điều kiện ta được ![]()
Vì m nguyên nên m = 2 hoặc m = 3.
Lời giải
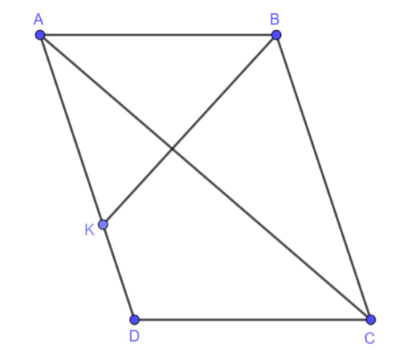
![]() nên AK = 2DK, K thuộc AD
nên AK = 2DK, K thuộc AD
Suy ra: 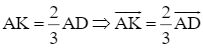
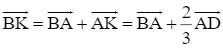
![]()
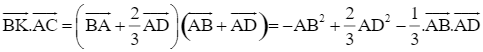
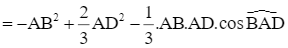
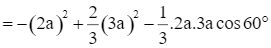
= a2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.