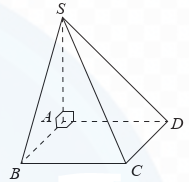
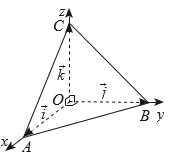
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và có độ dài bằng 1. Vẽ hệ trục toạ độ Oxyz có gốc là O, các điểm A, B, C lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục toạ độ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Với \(O\) là gốc toạ độ, ta vẽ được các trục Ox, Oy, Oz như Hình vẽ. Ba vectơ đơn vị trên ba trục lần lượt là \(\vec i = \overrightarrow {OA} ,\vec j = \overrightarrow {OB} ,\vec k = \overrightarrow {OC} \)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
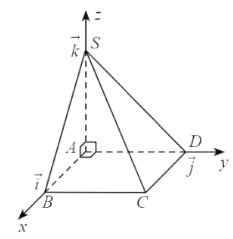
Trục \({\rm{Ox}}\) có vectơ đơn vị là \(\overrightarrow {AB} \).
Trục \({\rm{Oy}}\) có vectơ đơn vị là \(\overrightarrow {AD} \).
Trục \({\rm{Oz}}\) có vectơ đơn vị là \(\overrightarrow {AS} \).
Nhắn tin Zalo
Hỏi bài tập