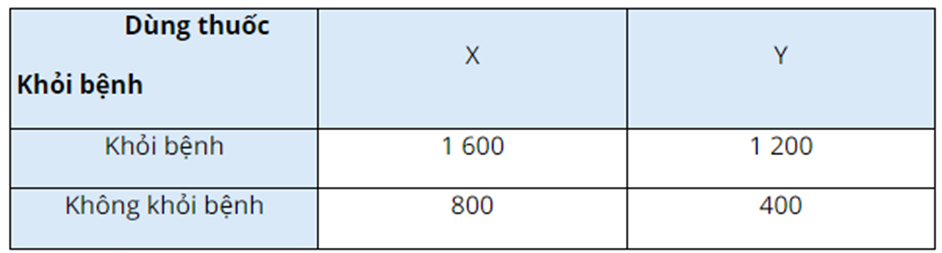
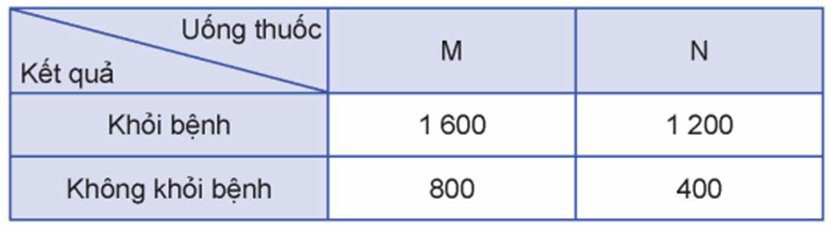
Từ công thức tính \(P(A\mid B)\) ở trên, chứng minh rằng nếu \(A\) và \(B\) là hai biến cố độc lập với \(P(A) > 0,P(B) > 0\) thì \(P(A\mid B) = P(A)\) và \(P(B\mid A) = P(B)\).
Từ công thức tính \(P(A\mid B)\) ở trên, chứng minh rằng nếu \(A\) và \(B\) là hai biến cố độc lập với \(P(A) > 0,P(B) > 0\) thì \(P(A\mid B) = P(A)\) và \(P(B\mid A) = P(B)\).
Quảng cáo
Trả lời:
Nếu \(A\) và \(B\) là hai biến cố độc lập thì \(P(AB) = P(A) \cdot P(B)\).
Vậy với \(P(A) > 0,P(B) > 0\) ta có:
\(P(A\mid B) = \frac{{P(AB)}}{{P(B)}} = \frac{{P(A) \cdot P(B)}}{{P(B)}} = P(A);\)
\(P(B\mid A) = \frac{{P(BA)}}{{P(A)}} = \frac{{P(B) \cdot P(A)}}{{P(A)}} = P(B).\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
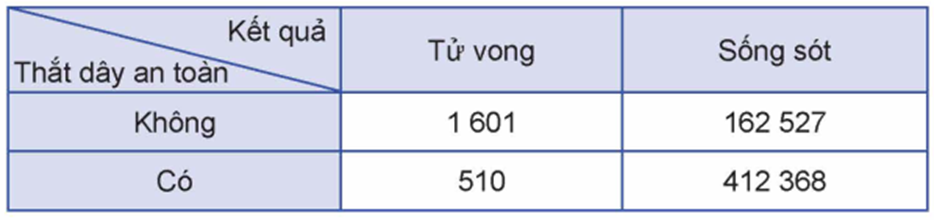
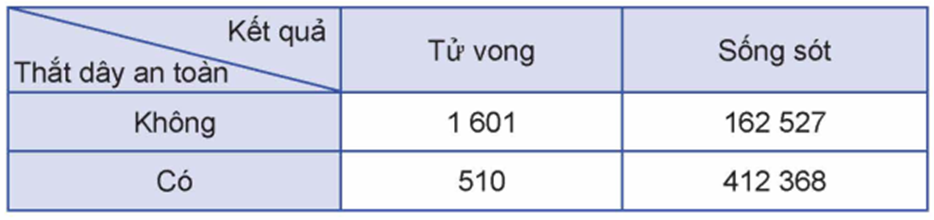
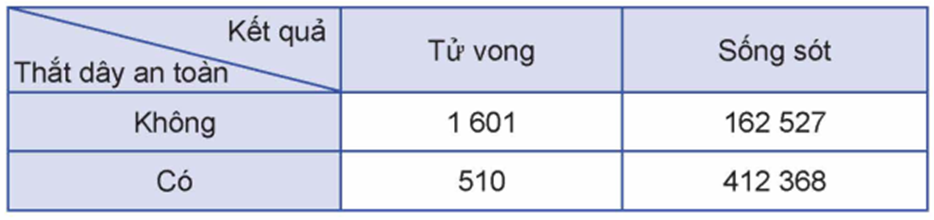
Ta cần tính \(P(A\mid \bar B)\).
\(\bar B\) là biến cố: "Người lái xe đó có thắt dây an toàn khi xảy ra tai nạn giao thông".
\(A\bar B\) là biến cố: "Người lái xe đó tử vong và có thắt dây an toàn khi xảy ra tai nạn giao thông".
Ta có \(412368 + 510 = 412878\) người lái xe có thắt dây an toàn \( \Rightarrow n(\bar B) = 412878\).
Trong số những người có thắt dây an toàn, có 510 người tử vong khi xảy ra tai nạn giao thông \( \Rightarrow n(A\bar B) = 510\).
Tương tự như trên, ta có: \(P(A\mid \bar B) = \frac{{P(A\bar B)}}{{P(\bar B)}} = \frac{{n(A\bar B)}}{{n(\bar B)}} = \frac{{510}}{{412878.}} \approx 1,235 \cdot {10^{ - 3}} = 0,001235.\)
Lời giải
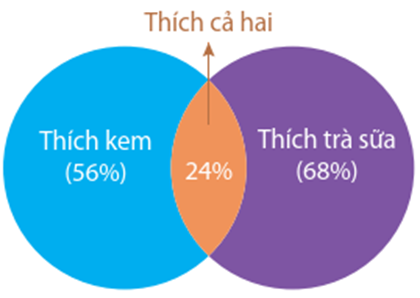
Gọi:
- A là biến cố "Chọn được học sinh thích kem";
- \(B\) là biến cố "Chọn được học sinh thích trà sữa".
Khi đó xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa chính là xác suất của \(A\) với điều kiện \(B\).
Vì có \(68\% \) số học sinh thích trà sữa trong nhóm khảo sát nên \(P(B) = 68\% = 0,68\).
Ta có AB là biến cố "Chọn được học sinh thích cả trà sửa và kem".
Vì có \(24\% \) số học sinh thích cả trà sữa và kem nên \(P(AB) = 24\% = 0,24\).
Vì thế ta có: \(P(A\mid B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,24}}{{0,68}} \approx 0,35\).
Vậy xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa là 0,35 .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.